In the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 area of knot theory

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

, the unknotting number of a knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

 is the minimum number of times the knot must be passed through itself to untie it. If a knot has unknotting number , then there exists a diagram of the knot which can be changed to unknot

Unknot

The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...

 by switching crossings. The unknotting number of a knot is always less than or equal to the crossing number

Crossing number (knot theory)

In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....

.

Any composite knot has unknotting number at least two, and therefore every knot with unknotting number one is a prime knot

Prime knot

In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...

. The following table show the unknotting numbers for the first few knots:

In general, it is relatively difficult to determine the unknotting number of a given knot. Known cases include:

• The unknotting number of a nontrivial twist knot
  Twist knot
  In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together...
  
   is always equal to one.
• The unknotting number of a -torus knot
  Torus knot
  In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
  
   is equal to .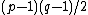
• The unknotting numbers of prime knot
  Prime knot
  In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
  
  s with nine or fewer crossings
  Crossing number (knot theory)
  In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
  
   have all been determined. (The unknotting number of the 10₁₁ prime knot is unknown.)

Other numerical knot invariants

• Crossing number
  Crossing number (knot theory)
  In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
  
  
• Bridge number
  Bridge number
  In a mathematical field of knot theory, the bridge number is an invariant of a knot. It is defined as the minimal number of bridges required in all the possible bridge representations of a knot...
  
  
• Linking coefficient
• Stick number
  Stick number
  In the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot...