Converse (logic)
Encyclopedia
In logic
, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication
P → Q, the converse is Q → P. For the categorical proposition
All S is P, the converse is All P is S. In neither case does the converse necessarily follow from the original statement. The categorical converse of a statement is contrasted with the contrapositive
and the obverse
.
P and the consequent
Q are logically equivalent.
For example, consider the true statement "If I am a human, then I am mortal." The converse of that statement is "If I am mortal, then I am a human," which is not necessarily true.
On the other hand, the converse of a statement with mutually inclusive terms remains true, given the truth of the original proposition. Thus, the statement "If I am a bachelor, then I am unmarried" is logically equivalent to "If I am unmarried, then I am a bachelor" (if "I" is assumed to be male).
A truth table makes it clear that S and the converse of S are not logically equivalent unless both terms imply each other:
Going from a statement to its converse is the fallacy of affirming the consequent
. However, if the statement S and its converse are equivalent (i.e. if P is true if and only if
Q is also true), then affirming the consequent will be valid.
was proved in 1912, but its converse only in 1998.
In practice, when determining the converse of a mathematical theorem, aspects of the antecedent may be taken as establishing context. That is, the converse of Given P, if Q then R will be Given P, if R then Q. For example, the Pythagorean theorem
can be stated as:
The converse, which also appears in Euclid's Elements
(Book I, Proposition 48), can be stated as:
, "The original proposition is called the exposita; when converted, it is denominated the converse. Conversion is valid when, and only when, nothing is asserted in the converse which is not affirmed or implied in the exposita." The "exposita" is more usually called the "convertend." In its simple form, conversion is valid only for E and I propositions:
The validity of simple conversion only for E and I propositions can be expressed by the restriction that "No term must be distributed in the converse which is not distributed in the convertend." For E propositions, both subject and predicate are distributed, while for I propositions, neither is.
For A propositions, the subject is distributed while the predicate is not, and so the inference from an A statement to its converse is not valid. As an example, for the A proposition "All cats are mammals," the converse "All mammals are cats" is obviously false. However, the weaker statement "Some mammals are cats" is true. Logicians define conversion per accidens to be the process of producing this weaker statement. Inference from a statement to its converse per accidens is generally valid. However, as with syllogism
s, this switch from the universal to the particular causes problems with empty categories: "All unicorns are mammals" is often taken as true, while the converse per accidens "Some mammals are unicorns" is clearly false.
In first-order predicate calculus
, All S is P can be represented as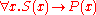
. It is therefore clear that the categorical converse is closely related to the implicational converse, and that S and P cannot be swapped in All S is P.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
P → Q, the converse is Q → P. For the categorical proposition
Categorical proposition
A categorical proposition contains two categorical terms, the subject and the predicate, and affirms or denies the latter of the former. Categorical propositions occur in categorical syllogisms and both are discussed in Aristotle's Prior Analytics....
All S is P, the converse is All P is S. In neither case does the converse necessarily follow from the original statement. The categorical converse of a statement is contrasted with the contrapositive
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
and the obverse
Obversion
In traditional logic, obversion is a "type of immediate inference in which from a given proposition another proposition is inferred whose subject is the same as the original subject, whose predicate is the contradictory of the original predicate, and whose quality is affirmative if the original...
.
Implicational converse
If S is a statement of the form P implies Q (P → Q), then the converse of S is the statement Q implies P (Q → P). In general, the verity of S says nothing about the verity of its converse, unless the antecedentAntecedent (logic)
An antecedent is the first half of a hypothetical proposition.Examples:* If P, then Q.This is a nonlogical formulation of a hypothetical proposition...
P and the consequent
Consequent
A consequent is the second half of a hypothetical proposition. In the standard form of such a proposition, it is the part that follows "then".Examples:* If P, then Q.Q is the consequent of this hypothetical proposition....
Q are logically equivalent.
For example, consider the true statement "If I am a human, then I am mortal." The converse of that statement is "If I am mortal, then I am a human," which is not necessarily true.
On the other hand, the converse of a statement with mutually inclusive terms remains true, given the truth of the original proposition. Thus, the statement "If I am a bachelor, then I am unmarried" is logically equivalent to "If I am unmarried, then I am a bachelor" (if "I" is assumed to be male).
A truth table makes it clear that S and the converse of S are not logically equivalent unless both terms imply each other:
| P | Q | P → Q | Q → P (converse) |
|---|---|---|---|
| T | T | T | T |
| T | F | F | T |
| F | T | T | F |
| F | F | T | T |
Going from a statement to its converse is the fallacy of affirming the consequent
Affirming the consequent
Affirming the consequent, sometimes called converse error, is a formal fallacy, committed by reasoning in the form:#If P, then Q.#Q.#Therefore, P....
. However, if the statement S and its converse are equivalent (i.e. if P is true if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
Q is also true), then affirming the consequent will be valid.
Converse of a theorem
In mathematics, the converse of a theorem of the form P → Q will be Q → P. The converse may or may not be true. If true, the proof may be difficult. For example, the Four-vertex theoremFour-vertex theorem
The four-vertex theorem states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema...
was proved in 1912, but its converse only in 1998.
In practice, when determining the converse of a mathematical theorem, aspects of the antecedent may be taken as establishing context. That is, the converse of Given P, if Q then R will be Given P, if R then Q. For example, the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
can be stated as:
Given a triangle with sides of length a, b, and c, if the angle opposite the side of length c is a right angle, then a2 + b2 = c2.
The converse, which also appears in Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
(Book I, Proposition 48), can be stated as:
Given a triangle with sides of length a, b, and c, if a2 + b2 = c2, then the angle opposite the side of length c is a right angle.
Categorical converse
In traditional logic, the process of going from All S is P to its converse All P is S is called conversion. In the words of Asa MahanAsa Mahan
Asa Mahan was a U.S. Congregational clergyman and educator and the first president of Oberlin College and Adrian College.-Career:...
, "The original proposition is called the exposita; when converted, it is denominated the converse. Conversion is valid when, and only when, nothing is asserted in the converse which is not affirmed or implied in the exposita." The "exposita" is more usually called the "convertend." In its simple form, conversion is valid only for E and I propositions:
| Type | Convertend | Simple converse | Converse per accidens |
|---|---|---|---|
| A | All S is P | not valid | Some P is S |
| E | No S is P | No P is S | Some P is not S |
| I | Some S is P | Some P is S | – |
| O | Some S is not P | not valid | – |
The validity of simple conversion only for E and I propositions can be expressed by the restriction that "No term must be distributed in the converse which is not distributed in the convertend." For E propositions, both subject and predicate are distributed, while for I propositions, neither is.
For A propositions, the subject is distributed while the predicate is not, and so the inference from an A statement to its converse is not valid. As an example, for the A proposition "All cats are mammals," the converse "All mammals are cats" is obviously false. However, the weaker statement "Some mammals are cats" is true. Logicians define conversion per accidens to be the process of producing this weaker statement. Inference from a statement to its converse per accidens is generally valid. However, as with syllogism
Syllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
s, this switch from the universal to the particular causes problems with empty categories: "All unicorns are mammals" is often taken as true, while the converse per accidens "Some mammals are unicorns" is clearly false.
In first-order predicate calculus
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, All S is P can be represented as
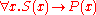. It is therefore clear that the categorical converse is closely related to the implicational converse, and that S and P cannot be swapped in All S is P.See also
- AristotleAristotleAristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
- ContrapositionContrapositionIn traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
- InferenceInferenceInference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
- ObversionObversionIn traditional logic, obversion is a "type of immediate inference in which from a given proposition another proposition is inferred whose subject is the same as the original subject, whose predicate is the contradictory of the original predicate, and whose quality is affirmative if the original...
- SyllogismSyllogismA syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
- Relational oppositenessRelational oppositenessIn linguistics the term relational oppositeness refers to the relationship between two words which seem to be opposites of each other but in fact actually imply each other. For example own and belong are relational opposites i.e. "A owns B" is the same as "B belongs to A" Other examples are above...
- SyllogismSyllogismA syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
- Term logicTerm logicIn philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
- Transposition (logic)Transposition (logic)In the methods of deductive reasoning in classical logic, transposition is the rule of inference that permits one to infer from the truth of "A implies B" the truth of "Not-B implies not-A", and conversely. Its symbolic expression is:...
- Inverse (logic)Inverse (logic)In traditional logic, an inverse is a type of conditional sentence which is an immediate inference made from another conditional sentence. Any conditional sentence has an inverse: the contrapositive of the converse. The inverse of P \rightarrow Q is thus \neg P \rightarrow \neg Q...
Further reading
- AristotleAristotleAristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
. Organon. - Copi, IrvingIrving CopiIrving Marmer Copi was an American philosopher, logician, and university textbook author....
. Introduction to Logic. MacMillan, 1953. - Copi, Irving. Symbolic Logic. MacMillan, 1979, fifth edition.
- Stebbing, SusanSusan StebbingL. Susan Stebbing was a British philosopher. She belonged to the 1930s generation of analytic philosophy, and was a founder in 1933 of the journal Analysis.-Biography:...
. A Modern Introduction to Logic. Cromwell Company, 1931.