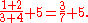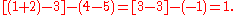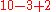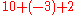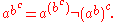Order of operations
Encyclopedia
In mathematics
and computer programming
, the order of operations (sometimes called operator precedence) is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression
.
For example, in mathematics and most computer languages multiplication is done before addition; in the expression 2 + 3 × 4, the answer is 14. Brackets, which have their own rules, may be used to avoid confusion, thus the preceding expression may also be rendered 2 + (3 × 4), but the brackets are not required as multiplication still has precedence without them.
From the introduction of modern algebraic notation, where juxtaposition indicates multiplication of variables, multiplication took precedence over addition, whichever side of a number it appeared on. Thus 3 + 4 × 5 = 4 × 5 + 3 = 23. When exponents were first introduced, in the 16th and 17th centuries, exponents took precedence over both addition and multiplication, and could be placed only as a superscript to the right of their base. Thus 3 + 52 = 28 and 3 × 52 = 75. To change the order of operations, originally a vinculum (an overline or underline) was used. Today we use brackets. Thus, to force addition to precede multiplication, we write (2 + 3) × 4 = 20, and to force addition to precede exponentiation, we write (3 + 5)2 = 64.
s is expressed here:
This means that if a mathematical expression is preceded by one operator and followed by another, the operator higher on the list should be applied first. The commutative and associative laws of addition and multiplication allow terms to be added in any order and factors to be multiplied in any order, but mixed operations must obey the standard order of operations.
It is helpful to treat division as multiplication by the reciprocal (multiplicative inverse) and subtraction as addition of the opposite (additive inverse). Thus 3/4 = 3 ÷ 4 = 3 • ¼; in other words the quotient of 3 and 4 equals the product of 3 and ¼. Also 3 − 4 = 3 + (−4); in other words the difference of 3 and 4 equals the sum of positive three and negative four. With this understanding, we can think of 1 - 2 + 3 as the sum of 1, negative 2, and 3, and add in any order: (1 - 2) + 3 = -1 + 3 = 2 and in reverse order (3 - 2) + 1 = 1 + 1 = 2. The important thing is to keep the negative sign with the 2.
The root symbol, √, requires a symbol of grouping around the radicand. The usual symbol of grouping is a bar (called vinculum) over the radicand. For the application of other functions, such as logarithm
or cosine, the grouping is advised and denoted by parenthesis or brackets.
Stacked exponents are applied from the top down.
Symbols of grouping can be used to override the usual order of operations. Grouped symbols can be treated as a single expression. Symbols of grouping can be removed using the associative and distributive laws.
A horizontal fractional line also acts as a symbol of grouping:
For ease in reading, other grouping symbols such as braces, sometimes called curly braces { }, or brackets, sometimes called square brackets [ ], are often used along with parentheses . For example,
, unary operators have a higher priority than binary operators, that is, the unary minus (negation) has higher precedence than exponentiation, so in those languages −32 will be interpreted as (−3)2 = 9. http://support.microsoft.com/kb/q132686/. In any case where there is a possibility that the notation might be misinterpreted, it is advisable to use brackets to clarify which interpretation is intended.
Similarly, care must be exercised when using the slash ('/') symbol. The string of characters "1/2x" is interpreted by the above conventions as (1/2)x. The contrary interpretation should be written explicitly as 1/(2x). Again, the use of brackets will clarify the meaning and should be used if there is any chance of misinterpretation.
Mnemonics are often used to help students remember the rules, but the rules taught by the use of acronyms can be misleading. In the United States the acronym PEMDAS is common. It stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. Canada uses BIDMAS
In Canada and other English speaking countries, Parentheses may be called Brackets, or symbols of inclusion and Exponentiation may be called either Indices, Powers or Orders, and since multiplication and division are of equal precedence, M and D are often interchanged, leading to such acronyms as BEDMAS, BIDMAS, BODMAS, BERDMAS, PERDMAS, and BPODMAS.
These mnemonics may be misleading when written this way, especially if the user is not aware that multiplication and division are of equal precedence, as are addition and subtraction. Using any of the above rules in the order "addition first, subtraction afterward" would also give the wrong answer.
The correct answer is 9 (and not 5, which we get when we add 3 and 2 first to get 5,and then subtract it from 10 to get the final ans as 5), which is best understood by thinking of the problem as the sum of positive ten, negative three, and positive two.
An alternative way to write the mnemonic is:
P
E
MD
AS
Or, simply as PEMA, where it is taught that multiplication and division inherently share the same precedence; and that addition and subtraction inherently share the same precedence. PEMA is one of the mnemonics taught in New Zealand.
This makes the equivalence of multiplication and division, and addition and subtraction, clear.
Once logs are introduced the mnemonic can be written as:
P
EL
MD
AS
of the term immediately to its left, before computing any of the lower-precedence operations, unless grouping symbols dictate otherwise. But 23! means (23)! = 8! = 40320 while 23! = 26 = 64; a factorial in an exponent applies to the exponent, while a factorial not in the exponent applies to the entire power.
If exponentiation is indicated by stacked symbols, the rule is to work from the top down, thus:
A function name usually applies to the monomial following the name, thus "sin xy" means sin (xy) but sin x + y means (sin x) + y. Calculators usually require brackets, and brackets should be used in complicated expressions to prevent misunderstanding.
Sometimes a dash or a heavy dot is used as a multiplication sign which has higher precedence than division.
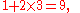
while more sophisticated calculators will use a more standard priority, for example giving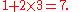
The Microsoft Calculator
program uses the former in its standard view and the latter in its scientific view.
The non-scientific calculator expects two operands and an operator. When the next operator is pressed, the expression is immediately evaluated and the answer becomes the left hand of the next operator. Advanced calculators allow entry of the whole expression, grouped as necessary, and only evaluates when the user uses the equals sign.
Calculators may associate exponents to the left or to the right depending on the model. For example, the expression a ^ b ^ c on the TI-92 and TI-30XII (both Texas Instruments calculators) associates two different ways:
The TI-92 associates to the right, that is
whereas, the TI-30XII associates to the left, that is
An expression like 1/2x is interpreted as 1/(2x) by TI-82, but as (1/2)x by TI-83. While the first interpretation may be expected by some users, only the latter is in agreement with the standard rules stated above.
, have no operator
precedence rules (in APL evaluation is strictly right to left, in Smalltalk
it's strictly left to right).
The logical bitwise operators in C
(and all programming languages that borrowed precedence rules from C, for example, C++
, Perl
and PHP
) have a precedence level that the creator of the C language considers to be unsatisfactory. However, many programmers have become accustomed to this order. The relative precedence levels of operators
found in many C-style languages are as follows:
Examples:
The accuracy of software developer knowledge about binary operator precedence has been found to closely follow their frequency of occurrence in source code.
See also
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer programming
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
, the order of operations (sometimes called operator precedence) is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
.
For example, in mathematics and most computer languages multiplication is done before addition; in the expression 2 + 3 × 4, the answer is 14. Brackets, which have their own rules, may be used to avoid confusion, thus the preceding expression may also be rendered 2 + (3 × 4), but the brackets are not required as multiplication still has precedence without them.
From the introduction of modern algebraic notation, where juxtaposition indicates multiplication of variables, multiplication took precedence over addition, whichever side of a number it appeared on. Thus 3 + 4 × 5 = 4 × 5 + 3 = 23. When exponents were first introduced, in the 16th and 17th centuries, exponents took precedence over both addition and multiplication, and could be placed only as a superscript to the right of their base. Thus 3 + 52 = 28 and 3 × 52 = 75. To change the order of operations, originally a vinculum (an overline or underline) was used. Today we use brackets. Thus, to force addition to precede multiplication, we write (2 + 3) × 4 = 20, and to force addition to precede exponentiation, we write (3 + 5)2 = 64.
The standard order of operations
The order of operations, or precedence, used in mathematics and many programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s is expressed here:
-
-
- terms inside parentheses or brackets
- exponentsExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
and rootsNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root... - multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and divisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
As they appear left to right
-
-
-
- additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
As they appear left to right
- addition
-
This means that if a mathematical expression is preceded by one operator and followed by another, the operator higher on the list should be applied first. The commutative and associative laws of addition and multiplication allow terms to be added in any order and factors to be multiplied in any order, but mixed operations must obey the standard order of operations.
It is helpful to treat division as multiplication by the reciprocal (multiplicative inverse) and subtraction as addition of the opposite (additive inverse). Thus 3/4 = 3 ÷ 4 = 3 • ¼; in other words the quotient of 3 and 4 equals the product of 3 and ¼. Also 3 − 4 = 3 + (−4); in other words the difference of 3 and 4 equals the sum of positive three and negative four. With this understanding, we can think of 1 - 2 + 3 as the sum of 1, negative 2, and 3, and add in any order: (1 - 2) + 3 = -1 + 3 = 2 and in reverse order (3 - 2) + 1 = 1 + 1 = 2. The important thing is to keep the negative sign with the 2.
The root symbol, √, requires a symbol of grouping around the radicand. The usual symbol of grouping is a bar (called vinculum) over the radicand. For the application of other functions, such as logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
or cosine, the grouping is advised and denoted by parenthesis or brackets.
Stacked exponents are applied from the top down.
Symbols of grouping can be used to override the usual order of operations. Grouped symbols can be treated as a single expression. Symbols of grouping can be removed using the associative and distributive laws.
Examples
A horizontal fractional line also acts as a symbol of grouping:
For ease in reading, other grouping symbols such as braces, sometimes called curly braces { }, or brackets, sometimes called square brackets [ ], are often used along with parentheses . For example,
Gaps in the standard
There exist differing conventions concerning the unary operator − (usually read "minus"). In written or printed mathematics, the expression −32 is interpreted to mean −(32) = −9, but in some applications and programming languages, notably the application Microsoft Office Excel and the programming language bcBc programming language
bc, for bench calculator, is "an arbitrary precision calculator language" with syntax similar to the C programming language. bc is typically used as either a mathematical scripting language or as an interactive mathematical shell....
, unary operators have a higher priority than binary operators, that is, the unary minus (negation) has higher precedence than exponentiation, so in those languages −32 will be interpreted as (−3)2 = 9. http://support.microsoft.com/kb/q132686/. In any case where there is a possibility that the notation might be misinterpreted, it is advisable to use brackets to clarify which interpretation is intended.
Similarly, care must be exercised when using the slash ('/') symbol. The string of characters "1/2x" is interpreted by the above conventions as (1/2)x. The contrary interpretation should be written explicitly as 1/(2x). Again, the use of brackets will clarify the meaning and should be used if there is any chance of misinterpretation.
Mnemonics
Mnemonics are often used to help students remember the rules, but the rules taught by the use of acronyms can be misleading. In the United States the acronym PEMDAS is common. It stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. Canada uses BIDMAS
In Canada and other English speaking countries, Parentheses may be called Brackets, or symbols of inclusion and Exponentiation may be called either Indices, Powers or Orders, and since multiplication and division are of equal precedence, M and D are often interchanged, leading to such acronyms as BEDMAS, BIDMAS, BODMAS, BERDMAS, PERDMAS, and BPODMAS.
These mnemonics may be misleading when written this way, especially if the user is not aware that multiplication and division are of equal precedence, as are addition and subtraction. Using any of the above rules in the order "addition first, subtraction afterward" would also give the wrong answer.
The correct answer is 9 (and not 5, which we get when we add 3 and 2 first to get 5,and then subtract it from 10 to get the final ans as 5), which is best understood by thinking of the problem as the sum of positive ten, negative three, and positive two.
An alternative way to write the mnemonic is:
P
E
MD
AS
Or, simply as PEMA, where it is taught that multiplication and division inherently share the same precedence; and that addition and subtraction inherently share the same precedence. PEMA is one of the mnemonics taught in New Zealand.
This makes the equivalence of multiplication and division, and addition and subtraction, clear.
Once logs are introduced the mnemonic can be written as:
P
EL
MD
AS
Special cases
An exclamation mark indicates that one should compute the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of the term immediately to its left, before computing any of the lower-precedence operations, unless grouping symbols dictate otherwise. But 23
If exponentiation is indicated by stacked symbols, the rule is to work from the top down, thus:
A function name usually applies to the monomial following the name, thus "sin xy" means sin (xy) but sin x + y means (sin x) + y. Calculators usually require brackets, and brackets should be used in complicated expressions to prevent misunderstanding.
Sometimes a dash or a heavy dot is used as a multiplication sign which has higher precedence than division.
Calculators
Different calculators follow different orders of operations. Most non-scientific calculators without a stack work left to right without any priority given to different operators, for example giving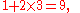
while more sophisticated calculators will use a more standard priority, for example giving
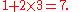
The Microsoft Calculator
Microsoft Calculator
Windows Calculator, commonly known as Calculator from the application's title bar, is a calculation application included in all versions of the Microsoft Windows operating system...
program uses the former in its standard view and the latter in its scientific view.
The non-scientific calculator expects two operands and an operator. When the next operator is pressed, the expression is immediately evaluated and the answer becomes the left hand of the next operator. Advanced calculators allow entry of the whole expression, grouped as necessary, and only evaluates when the user uses the equals sign.
Calculators may associate exponents to the left or to the right depending on the model. For example, the expression a ^ b ^ c on the TI-92 and TI-30XII (both Texas Instruments calculators) associates two different ways:
The TI-92 associates to the right, that is
-
- a ^ b ^ c = a ^ (b ^ c) =
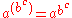
- a ^ b ^ c = a ^ (b ^ c) =
whereas, the TI-30XII associates to the left, that is
-
- a ^ b ^ c = (a ^ b) ^ c =
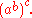
- a ^ b ^ c = (a ^ b) ^ c =
An expression like 1/2x is interpreted as 1/(2x) by TI-82, but as (1/2)x by TI-83. While the first interpretation may be expected by some users, only the latter is in agreement with the standard rules stated above.
Programming languages
Many programming languages use precedence levels that conform to the order commonly used in mathematics, though some, such as APL and SmalltalkSmalltalk
Smalltalk is an object-oriented, dynamically typed, reflective programming language. Smalltalk was created as the language to underpin the "new world" of computing exemplified by "human–computer symbiosis." It was designed and created in part for educational use, more so for constructionist...
, have no operator
Operator (programming)
Programming languages typically support a set of operators: operations which differ from the language's functions in calling syntax and/or argument passing mode. Common examples that differ by syntax are mathematical arithmetic operations, e.g...
precedence rules (in APL evaluation is strictly right to left, in Smalltalk
Smalltalk
Smalltalk is an object-oriented, dynamically typed, reflective programming language. Smalltalk was created as the language to underpin the "new world" of computing exemplified by "human–computer symbiosis." It was designed and created in part for educational use, more so for constructionist...
it's strictly left to right).
The logical bitwise operators in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
(and all programming languages that borrowed precedence rules from C, for example, C++
C++
C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, Perl
Perl
Perl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
and PHP
PHP
PHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
) have a precedence level that the creator of the C language considers to be unsatisfactory. However, many programmers have become accustomed to this order. The relative precedence levels of operators
Operator (programming)
Programming languages typically support a set of operators: operations which differ from the language's functions in calling syntax and/or argument passing mode. Common examples that differ by syntax are mathematical arithmetic operations, e.g...
found in many C-style languages are as follows:
| 1 | [] -> . :: | Grouping, scope, array/member access | |
| 2 | ! ~ - + * & sizeof type cast ++x --x | (most) unary operations, sizeof and type casts | |
| 3 | * / % | Multiplication, division, modulo Modular arithmetic In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus.... |
|
| 4 | + - | Addition and subtraction | |
| 5 | << >> | Bitwise shift left and right | |
| 6 | < <= > >= | Comparisons: less-than, ... | |
| 7 | != | Comparisons: equal and not equal | |
| 8 | & | Bitwise AND | |
| 9 | ^ | Bitwise exclusive OR | |
| 10 | > | Bitwise inclusive (normal) OR | |
| 11 | && | Logical AND | |
| 12 | |
Logical OR | |
| 13 | ?: | Conditional expression ?: In computer programming, ?: is a ternary operator that is part of the syntax for a basic conditional expression in several programming languages... (ternary operator) |
|
| 14 | >= ^= <<= >>= | Assignment operators | |
| 15 | , | Comma operator Comma operator In the C and C++ programming languages, the comma operator is a binary operator that evaluates its first operand and discards the result, and then evaluates the second operand and returns this value... |
Examples:
-
!A + !B
(!A) + (!B) -
++A + !B
(++A) + (!B) -
A * B + C
(A * B) + C -
A || B && C
A || (B && C) -
( A && B C )
( A && ( BC ) )
The accuracy of software developer knowledge about binary operator precedence has been found to closely follow their frequency of occurrence in source code.
See also
- Common operator notationCommon operator notationIn programming languages, common operator notation is one way of notating mathematical expressions as a linear sequence of tokens, or operators.In this model, tokens are divided into two classes: operators and operands....
(for a more formal description) - Operator associativityOperator associativityIn programming languages and mathematical notation, the associativity of an operator is a property that determines how operators of the same precedence are grouped in the absence of parentheses...
- AssociativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
- CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
- DistributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
- Operator (programming)Operator (programming)Programming languages typically support a set of operators: operations which differ from the language's functions in calling syntax and/or argument passing mode. Common examples that differ by syntax are mathematical arithmetic operations, e.g...
- Operator overloadingOperator overloadingIn object oriented computer programming, operator overloading—less commonly known as operator ad-hoc polymorphism—is a specific case of polymorphism, where different operators have different implementations depending on their arguments...
- Operator precedence in C and C++
- Reverse Polish NotationReverse Polish notationReverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...