
Monogenic semigroup
Encyclopedia
In mathematics
, a monogenic semigroup is a semigroup
generated by a set containing only a single element. Monogenic semigroups are also called cyclic semigroups.
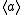 . The set of elements of
. The set of elements of  is { a, a2, a3, ... }. There are two possibilities for the monogenic semigroup
is { a, a2, a3, ... }. There are two possibilities for the monogenic semigroup 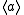 :
:
In the former case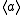 is isomorphic to the semigroup ( {1, 2, ... }, + ) of natural numbers under addition
is isomorphic to the semigroup ( {1, 2, ... }, + ) of natural numbers under addition
. In such a case, is an infinite monogenic semigroup and the element a has infinite order.
is an infinite monogenic semigroup and the element a has infinite order.
In the latter case let m be the smallest positive integer such that a m = a x for some positive integer x ≠ m, and let r be smallest positive integer such that a m = a m + r. The positive integer m is referred to as the index and the positive integer r as the period of the monogenic semigroup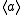 . The period and the index satisfy the following properties:
. The period and the index satisfy the following properties:
The pair ( m, r ) of positive integers determine the structure
of monogenic semigroups. For every pair ( m, r ) of positive integers, there does exist a monogenic semigroup having index m and period r. The monogenic semigroup having index m and period r is denoted by M ( m, r ). The monogenic semigroup M ( 1, r ) is the cyclic group
of order r.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a monogenic semigroup is a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
generated by a set containing only a single element. Monogenic semigroups are also called cyclic semigroups.
Structure
The monogenic semigroup generated by the singleton set { a } is denoted by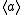 . The set of elements of
. The set of elements of  is { a, a2, a3, ... }. There are two possibilities for the monogenic semigroup
is { a, a2, a3, ... }. There are two possibilities for the monogenic semigroup 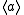 :
:
- a m = a n ⇒ m = n.
- There exist m ≠ n such that a m = a n.
In the former case
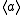 is isomorphic to the semigroup ( {1, 2, ... }, + ) of natural numbers under addition
is isomorphic to the semigroup ( {1, 2, ... }, + ) of natural numbers under additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
. In such a case,
 is an infinite monogenic semigroup and the element a has infinite order.
is an infinite monogenic semigroup and the element a has infinite order.In the latter case let m be the smallest positive integer such that a m = a x for some positive integer x ≠ m, and let r be smallest positive integer such that a m = a m + r. The positive integer m is referred to as the index and the positive integer r as the period of the monogenic semigroup
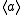 . The period and the index satisfy the following properties:
. The period and the index satisfy the following properties:
- a m = a m + r
- a m + x = a m + y if and only if m + x ≡ m + y ( mod r )
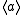 = { a, a2, ... , a m + r − 1 }
= { a, a2, ... , a m + r − 1 }- Ka = { am, a m + 1, ... , a m + r − 1 } is a cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of .
.
The pair ( m, r ) of positive integers determine the structure
Structure
Structure is a fundamental, tangible or intangible notion referring to the recognition, observation, nature, and permanence of patterns and relationships of entities. This notion may itself be an object, such as a built structure, or an attribute, such as the structure of society...
of monogenic semigroups. For every pair ( m, r ) of positive integers, there does exist a monogenic semigroup having index m and period r. The monogenic semigroup having index m and period r is denoted by M ( m, r ). The monogenic semigroup M ( 1, r ) is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order r.

