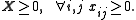Nonnegative matrix
Encyclopedia
A nonnegative matrix is a matrix
in which all the elements are equal to or greater than zero
A positive matrix is a matrix in which all the elements are greater than zero. The set of positive matrices is a subset of all non-negative matrices.
A non-negative matrix can represent a transition matrix for a Markov chain
.
A rectangular non-negative matrix can be approximated by a decomposition with two other non-negative matrices via non-negative matrix factorization.
A positive matrix is not the same as a positive-definite matrix
.
A matrix that is both non-negative and positive semidefinite is called a doubly non-negative matrix.
Eigenvalues and eigenvectors of square positive matrices are described by the Perron–Frobenius theorem
.
is a non-negative matrix. If the non-singular M-matrix is also symmetric then it is called a Stieltjes matrix
.
The inverse of a non-negative matrix is usually not non-negative. The exception is the non-negative monomial matrices: a non-negative matrix has non-negative inverse if and only if it is a (non-negative) monomial matrix. Note that thus the inverse of a positive matrix is not positive or even non-negative, as positive matrices are not monomial, for dimension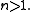
; doubly stochastic matrix
; symmetric non-negative matrix.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in which all the elements are equal to or greater than zero
A positive matrix is a matrix in which all the elements are greater than zero. The set of positive matrices is a subset of all non-negative matrices.
A non-negative matrix can represent a transition matrix for a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
.
A rectangular non-negative matrix can be approximated by a decomposition with two other non-negative matrices via non-negative matrix factorization.
A positive matrix is not the same as a positive-definite matrix
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
A matrix that is both non-negative and positive semidefinite is called a doubly non-negative matrix.
Eigenvalues and eigenvectors of square positive matrices are described by the Perron–Frobenius theorem
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
.
Inversion
The inverse of any non-singular M-matrixM-matrix
In mathematics, especially linear algebra, an M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices In mathematics, especially linear algebra, an M-matrix is a Z-matrix with...
is a non-negative matrix. If the non-singular M-matrix is also symmetric then it is called a Stieltjes matrix
Stieltjes matrix
In mathematics, particularly matrix theory, a Stieltjes matrix, named after Thomas Joannes Stieltjes, is a real symmetric positive definite matrix with nonpositive off-diagonal entries. A Stieltjes matrix is necessarily an M-matrix...
.
The inverse of a non-negative matrix is usually not non-negative. The exception is the non-negative monomial matrices: a non-negative matrix has non-negative inverse if and only if it is a (non-negative) monomial matrix. Note that thus the inverse of a positive matrix is not positive or even non-negative, as positive matrices are not monomial, for dimension
Specializations
There are a number of groups of matrices that form specializations of non-negative matrices, e.g. stochastic matrixStochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
; doubly stochastic matrix
Doubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
; symmetric non-negative matrix.