
Rational root theorem
Encyclopedia
In algebra
, the rational root theorem (or rational root test) states a constraint on rational solutions (or roots) of the polynomial
equation
with integer
coefficients.
If a0 and an are nonzero,
then each rational
solution x,
when written as a fraction x = p/q in lowest terms (i.e., the greatest common divisor of p and q is 1), satisfies
Thus, a list of possible rational roots of the equation can be derived using the formula .
.
The rational root theorem is a special case (for a single linear factor) of Gauss's lemma
on the factorization of polynomials. The integral root theorem is a special case of the rational root theorem if the leading coefficient an = 1.
p, q ∈ Z:
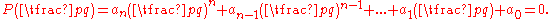
If we shift the constant term to the right hand side and multiply by qn, we get
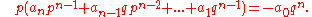
We see that p times the integer quantity in parentheses equals -a0qn, so p divides a0qn. But p is coprime to q and therefore to qn, so by (the generalized form of) Euclid's lemma
it must divide the remaining factor a0 of the product.
If we instead shift the leading term to the right hand side and multiply by qn, we get
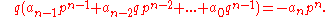
And for similar reasons, we can conclude that q divides an.
of the coefficients so as to obtain a primitive polynomial in the sense of Gauss's lemma
; this does not alter the set of rational roots and only strengthens the divisibility conditions. That lemma says that if the polynomial factors in , then it also factors in as a product of primitive polynomials. Now any rational root corresponds to a factor of degree 1 in of the polynomial, and its primitive representative is then , assuming that p and q are coprime. But any multiple in of has leading term divisible by q and constant term divisible by p, which proves the statement. This argument shows that more generally, any irreducible factor of P can be supposed to have integer coefficients, and leading and constant coefficients dividing the corresponding coefficients of P.

must be among the numbers symbolically indicated by
which gives the list of possible answers: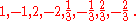
These root candidates can be tested using the Horner scheme
(for instance). In this particular case there is exactly one rational root. If a root candidate does not satisfy the equation, it can be used to shorten the list of remaining candidates. For example, x = 1 does not satisfy the equation as the left hand side equals 1. This means that substituting x = 1 + t yields a polynomial in t with constant term 1, while the coefficient of t3 remains the same as the coefficient of x3. Applying the rational root theorem thus yields the following possible roots for t: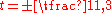
Therefore,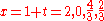
Root candidates that do not occur on both lists are ruled out. The list of rational root candidates has thus shrunk to just x = 2 and x = 2/3.
If a root r1
is found, the Horner scheme will also yield a polynomial of degree n − 1 whose roots, together with r1, are exactly the roots of the original polynomial. It may also be the case that none of the candidates is a solution; in this case the equation has no rational solution. If the equation lacks a constant term a0, then 0 is one of the rational roots of the equation.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the rational root theorem (or rational root test) states a constraint on rational solutions (or roots) of the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation

with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients.
If a0 and an are nonzero,
then each rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
solution x,
when written as a fraction x = p/q in lowest terms (i.e., the greatest common divisor of p and q is 1), satisfies
- p is an integer factorDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of the constant termConstant termIn mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
a0, and - q is an integer factor of the leading coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
an.
Thus, a list of possible rational roots of the equation can be derived using the formula
 .
.The rational root theorem is a special case (for a single linear factor) of Gauss's lemma
Gauss's lemma (polynomial)
In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
on the factorization of polynomials. The integral root theorem is a special case of the rational root theorem if the leading coefficient an = 1.
An elementary proof
Let P(x) = anxn + an-1xn-1 + ... + a1x + a0 for some a0, ..., an ∈ Z, and suppose P(p/q) = 0 for some coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
p, q ∈ Z:
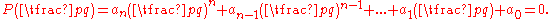
If we shift the constant term to the right hand side and multiply by qn, we get
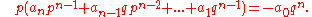
We see that p times the integer quantity in parentheses equals -a0qn, so p divides a0qn. But p is coprime to q and therefore to qn, so by (the generalized form of) Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
it must divide the remaining factor a0 of the product.
If we instead shift the leading term to the right hand side and multiply by qn, we get
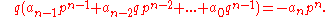
And for similar reasons, we can conclude that q divides an.
Proof using Gauss's lemma
Should there be a nontrivial factor dividing all the coefficients of the polynomial, then one can divide by the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of the coefficients so as to obtain a primitive polynomial in the sense of Gauss's lemma
Gauss's lemma
Gauss's lemma can mean any of several lemmas named after Carl Friedrich Gauss:* Gauss's lemma * Gauss's lemma * Gauss's lemma...
; this does not alter the set of rational roots and only strengthens the divisibility conditions. That lemma says that if the polynomial factors in , then it also factors in as a product of primitive polynomials. Now any rational root corresponds to a factor of degree 1 in of the polynomial, and its primitive representative is then , assuming that p and q are coprime. But any multiple in of has leading term divisible by q and constant term divisible by p, which proves the statement. This argument shows that more generally, any irreducible factor of P can be supposed to have integer coefficients, and leading and constant coefficients dividing the corresponding coefficients of P.
Example
For example, every rational solution of the equation
must be among the numbers symbolically indicated by
- ±

which gives the list of possible answers:
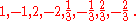
These root candidates can be tested using the Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
(for instance). In this particular case there is exactly one rational root. If a root candidate does not satisfy the equation, it can be used to shorten the list of remaining candidates. For example, x = 1 does not satisfy the equation as the left hand side equals 1. This means that substituting x = 1 + t yields a polynomial in t with constant term 1, while the coefficient of t3 remains the same as the coefficient of x3. Applying the rational root theorem thus yields the following possible roots for t:
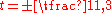
Therefore,
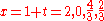
Root candidates that do not occur on both lists are ruled out. The list of rational root candidates has thus shrunk to just x = 2 and x = 2/3.
If a root r1
is found, the Horner scheme will also yield a polynomial of degree n − 1 whose roots, together with r1, are exactly the roots of the original polynomial. It may also be the case that none of the candidates is a solution; in this case the equation has no rational solution. If the equation lacks a constant term a0, then 0 is one of the rational roots of the equation.
See also
- Descartes' rule of signsDescartes' rule of signsIn mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
- Gauss–Lucas theorem
- Properties of polynomial roots
- Content (algebra)Content (algebra)In algebra, the content of a polynomial is the highest common factor of its coefficients.A polynomial is primitive if it has content unity....
External links
- RationalRootTheorem at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Another proof that nth roots of integers are irrational, except for perfect nth powers by Scott E. Brodie
- The Rational Roots Test at purplemath.com

