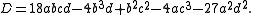Casus irreducibilis
Encyclopedia
In algebra
, casus irreducibilis (Latin
for "the irreducible case") is one of the cases that may arise in attempting to solve a cubic equation with integer
coefficients with roots that are expressed with radicals
. Specifically, if a cubic polynomial is irreducible
over the rational numbers and has three real roots, then in order to express the roots with radicals, one must introduce complex-valued expressions, even though the resulting expressions are ultimately real-valued. Casus irreducibilis was the original reason for the introduction of the complex number system by Niccolò Fontana Tartaglia
and Gerolamo Cardano
in 1545. The term imaginary number
referred then to a number which was imagined to exist in order to form an expression of the root.
One can decide whether a given irreducible cubic polynomial is in casus irreducibilis using the discriminant
D, via Cardano's formula. Let the cubic equation be given by
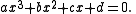
Then the discriminant D appearing in the algebraic solution is given by
, and that p(x) ∈ F[x] is a cubic polynomial, irreducible over F, but having three real roots (roots in the real closure of F). Then casus irreducibilis states that it is impossible to find any solution of p(x) = 0 by real radicals.
To prove this, note that the discriminant D is positive. Form the field extension
F(√D). Since this is a quadratic extension, p(x) remains irreducible in it. Consequently, the Galois group
of p(x) over F(√D) is the cyclic group C3. Suppose that p(x) = 0 can be solved by real radicals. Then p(x) can be split by a tower of cyclic extensions (of prime degree)
At the final step of the tower, p(x) is irreducible in the penultimate field K, but splits in K(∛α) for some α. But this is a cyclic field extension, and so must contain a primitive root of unity.
However, there are no primitive 3rd roots of unity in a real closed field. Indeed, suppose that ω is a primitive 3rd root of unity. Then, by the axioms defining an ordered field
, ω, ω2, and 1 are all positive. But if ω2>ω, then cubing both sides gives 1>1, a contradiction; similarly if ω>ω2.
which is an extension of F by radicals. Then the degree of p is a power of 2, and its splitting field is an iterated quadratic extension of F.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, casus irreducibilis (Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
for "the irreducible case") is one of the cases that may arise in attempting to solve a cubic equation with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients with roots that are expressed with radicals
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
. Specifically, if a cubic polynomial is irreducible
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the rational numbers and has three real roots, then in order to express the roots with radicals, one must introduce complex-valued expressions, even though the resulting expressions are ultimately real-valued. Casus irreducibilis was the original reason for the introduction of the complex number system by Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
and Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
in 1545. The term imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
referred then to a number which was imagined to exist in order to form an expression of the root.
One can decide whether a given irreducible cubic polynomial is in casus irreducibilis using the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
D, via Cardano's formula. Let the cubic equation be given by
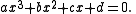
Then the discriminant D appearing in the algebraic solution is given by
- If D < 0, then the polynomial has two complex roots, so casus irreducibilis does not apply.
- If D = 0, then there are three real roots, and two of them are equal and can be found by the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
and the quadratic formula. All roots are real and expressible by real radicals. The polynomial is not irreducible. - If D > 0, then there are three distinct real roots. Either a rational root exists and can be found using the rational root test, in which case the cubic polynomial can be factored into the product of a linear polynomial and a quadratic polynomial, the latter of which can be solved via the quadratic formula; or no such factorization can occur, so the polynomial is the casus irreducibilis: all roots are real, but require complex numbers to express them in radicals.
Formal statement and proof
More generally, suppose that F is a formally real fieldFormally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
, and that p(x) ∈ F[x] is a cubic polynomial, irreducible over F, but having three real roots (roots in the real closure of F). Then casus irreducibilis states that it is impossible to find any solution of p(x) = 0 by real radicals.
To prove this, note that the discriminant D is positive. Form the field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
F(√D). Since this is a quadratic extension, p(x) remains irreducible in it. Consequently, the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of p(x) over F(√D) is the cyclic group C3. Suppose that p(x) = 0 can be solved by real radicals. Then p(x) can be split by a tower of cyclic extensions (of prime degree)
At the final step of the tower, p(x) is irreducible in the penultimate field K, but splits in K(∛α) for some α. But this is a cyclic field extension, and so must contain a primitive root of unity.
However, there are no primitive 3rd roots of unity in a real closed field. Indeed, suppose that ω is a primitive 3rd root of unity. Then, by the axioms defining an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, ω, ω2, and 1 are all positive. But if ω2>ω, then cubing both sides gives 1>1, a contradiction; similarly if ω>ω2.
Generalization
Casus irreducibilis can be generalized to higher degree polynomials as follows. Let p ∈ F[x] be an irreducible polynomial which splits in a formally real extension R of F (i.e., p has only real roots). Assume that p has a root in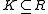 which is an extension of F by radicals. Then the degree of p is a power of 2, and its splitting field is an iterated quadratic extension of F.