
Trigonometric interpolation
Encyclopedia
In mathematics
, trigonometric interpolation is interpolation
with trigonometric polynomial
s. Interpolation is the process of finding a function which goes through some given data points. For trigonometric interpolation, this function has to be a trigonometric polynomial, that is, a sum of sines and cosines
of given periods. This form is especially suited for interpolation of periodic function
s.
An important special case is when the given data points are equally spaced, in which case the solution is given by the discrete Fourier transform
.
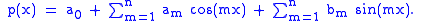
This expression contains 2n + 1 coefficients, a0, a1, … an, b1, …, bn, and we wish to compute those coefficients so that the function passes through N points:
Since the trigonometric polynomial is periodic with period 2π, it makes sense to assume that
(Note that we do not in general require these points to be equally spaced.) The interpolation problem is now to find coefficients such that the trigonometric polynomial p satisfies the interpolation conditions.
The solution can be written in a form similar to the Lagrange formula for polynomial interpolation
: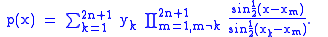
This can be shown to be a trigonometric polynomial by employing the multiple-angle formula and other identities for sin ½(x − xm).
. We can rewrite the formula for a trigonometric polynomial as
where i is the imaginary unit
. If we set z = eix, then this becomes
This reduces the problem of trigonometric interpolation to that of polynomial interpolation on the unit circle
. Existence and uniqueness for trigonometric interpolation now follows immediately from the corresponding results for polynomial interpolation.
For more information on formulation of trigonometric interpolating polynomials in the complex plane see , p128 Interpolation using Fourier Polynomials.
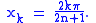
The transformation that maps the data points yk to the coefficients am, bm is known as the discrete Fourier transform
(DFT) of order 2n + 1.
(Because of the way the problem was formulated above, we have restricted ourselves to odd numbers of points. This is not strictly necessary; for even numbers of points, one includes another cosine term corresponding to the Nyquist frequency
.)
The case of the cosine-only interpolation for equally spaced points, corresponding to a trigonometric interpolation when the points have even symmetry
, was treated by Alexis Clairaut in 1754. In this case the solution is equivalent to a discrete cosine transform
. The sine-only expansion for equally spaced points, corresponding to odd symmetry, was solved by Joseph Louis Lagrange
in 1762, for which the solution is a discrete sine transform
. The full cosine and sine interpolating polynomial, which gives rise to the DFT, was solved by Carl Friedrich Gauss
in unpublished work around 1805, at which point he also derived a fast Fourier transform algorithm to evaluate it rapidly. Clairaut, Lagrange, and Gauss were all concerned with studying the problem of inferring the orbit
of planet
s, asteroid
s, etc., from a finite set of observation points; since the orbits are periodic, a trigonometric interpolation was a natural choice. See also Heideman et al. (1984).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, trigonometric interpolation is interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
with trigonometric polynomial
Trigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin and cos with n a natural number. The coefficients may be taken as real numbers, for real-valued functions...
s. Interpolation is the process of finding a function which goes through some given data points. For trigonometric interpolation, this function has to be a trigonometric polynomial, that is, a sum of sines and cosines
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
of given periods. This form is especially suited for interpolation of periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s.
An important special case is when the given data points are equally spaced, in which case the solution is given by the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
Formulation of the interpolation problem
A trigonometric polynomial of degree n has the form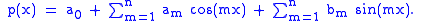
This expression contains 2n + 1 coefficients, a0, a1, … an, b1, …, bn, and we wish to compute those coefficients so that the function passes through N points:

Since the trigonometric polynomial is periodic with period 2π, it makes sense to assume that

(Note that we do not in general require these points to be equally spaced.) The interpolation problem is now to find coefficients such that the trigonometric polynomial p satisfies the interpolation conditions.
Solution of the problem
Under the above conditions, there exists a solution to the problem for any given set of data points {xk, p(xk)} as long as N, the number of data points, is not larger than the number of coefficients in the polynomial, i.e., N ≤ 2n+1 (a solution may or may not exist if N>2n+1 depending upon the particular set of data points). Moreover, the interpolating polynomial is unique if and only if the number of adjustable coefficients is equal to the number of data points, i.e., N = 2n + 1. In the remainder of this article, we will assume this condition to hold true.The solution can be written in a form similar to the Lagrange formula for polynomial interpolation
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
:
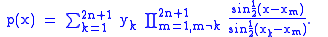
This can be shown to be a trigonometric polynomial by employing the multiple-angle formula and other identities for sin ½(x − xm).
Formulation in the complex plane
The problem becomes more natural if we formulate it in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. We can rewrite the formula for a trigonometric polynomial as

where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. If we set z = eix, then this becomes

This reduces the problem of trigonometric interpolation to that of polynomial interpolation on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. Existence and uniqueness for trigonometric interpolation now follows immediately from the corresponding results for polynomial interpolation.
For more information on formulation of trigonometric interpolating polynomials in the complex plane see , p128 Interpolation using Fourier Polynomials.
Equidistant nodes and the discrete Fourier transform
The special case in which the points xk are equally spaced is especially important. In this case, we have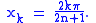
The transformation that maps the data points yk to the coefficients am, bm is known as the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) of order 2n + 1.
(Because of the way the problem was formulated above, we have restricted ourselves to odd numbers of points. This is not strictly necessary; for even numbers of points, one includes another cosine term corresponding to the Nyquist frequency
Nyquist frequency
The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
.)
The case of the cosine-only interpolation for equally spaced points, corresponding to a trigonometric interpolation when the points have even symmetry
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
, was treated by Alexis Clairaut in 1754. In this case the solution is equivalent to a discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
. The sine-only expansion for equally spaced points, corresponding to odd symmetry, was solved by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1762, for which the solution is a discrete sine transform
Discrete sine transform
In mathematics, the discrete sine transform is a Fourier-related transform similar to the discrete Fourier transform , but using a purely real matrix...
. The full cosine and sine interpolating polynomial, which gives rise to the DFT, was solved by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in unpublished work around 1805, at which point he also derived a fast Fourier transform algorithm to evaluate it rapidly. Clairaut, Lagrange, and Gauss were all concerned with studying the problem of inferring the orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
of planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s, asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
s, etc., from a finite set of observation points; since the orbits are periodic, a trigonometric interpolation was a natural choice. See also Heideman et al. (1984).

