List of small groups
Encyclopedia
The following list in mathematics
contains the finite group
s of small order
up to
group isomorphism
.
The list can be used to determine which known group a given finite group G is isomorphic to: first determine the order of G, then look up the candidates for that order in the list below. If you know whether G is abelian or not, some candidates can be eliminated right away. To distinguish between the remaining candidates, look at the orders of your group's elements, and match it with the orders of the candidate group's elements.
The notations Zn and Dihn have the advantage that point groups in three dimensions
Cn and Dn do not have the same notation. There are more isometry group
s than these two, of the same abstract group type.
The notation G × H stands for the direct product
of the two groups; Gn denotes the direct product of a group with itself n times. G
H stands for a semidirect product
where H acts on G; where the particular action of H on G is omitted, it is because all possible non-trivial actions result in the same product group, up to isomorphism.
Abelian
and simple group
s are noted. (For groups of order n < 60, the simple groups are precisely the cyclic groups Zn, for prime n.) The equality sign ("=") denotes isomorphism.
The identity element in the cycle graphs
is represented by the black circle. The lowest order for which the cycle graph does not uniquely represent a group is order 16.
In the lists of subgroups the trivial group and the group itself are not listed. Where there are multiple isomorphic subgroups, their number is indicated in parentheses.
s.
GAP
contains the "Small Groups library" which provides access to descriptions of small order groups. The groups are listed up to
isomorphism
. At present, the library contains the following groups:
It contains explicit descriptions of the available groups in computer readable format.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
contains the finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s of small order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
.
The list can be used to determine which known group a given finite group G is isomorphic to: first determine the order of G, then look up the candidates for that order in the list below. If you know whether G is abelian or not, some candidates can be eliminated right away. To distinguish between the remaining candidates, look at the orders of your group's elements, and match it with the orders of the candidate group's elements.
Glossary
- Zn: the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n (often the notation Cn is used, it is isomorphic to Z/nZ). - Dihn: the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 2n (often the notation Dn or D2n is used ) - Sn: the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of degree n, containing the n!FactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of n elements. - An: the alternating group of degree n, containing the n!/2 even permutations of n elements.
- Dicn: the dicyclic group of order 4n.
The notations Zn and Dihn have the advantage that point groups in three dimensions
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
Cn and Dn do not have the same notation. There are more isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
s than these two, of the same abstract group type.
The notation G × H stands for the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the two groups; Gn denotes the direct product of a group with itself n times. G
H stands for a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
where H acts on G; where the particular action of H on G is omitted, it is because all possible non-trivial actions result in the same product group, up to isomorphism.
Abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
and simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s are noted. (For groups of order n < 60, the simple groups are precisely the cyclic groups Zn, for prime n.) The equality sign ("=") denotes isomorphism.
The identity element in the cycle graphs
Cycle graph (algebra)
In group theory, a sub-field of abstract algebra, a group cycle graph illustrates the various cycles of a group and is particularly useful in visualizing the structure of small finite groups...
is represented by the black circle. The lowest order for which the cycle graph does not uniquely represent a group is order 16.
In the lists of subgroups the trivial group and the group itself are not listed. Where there are multiple isomorphic subgroups, their number is indicated in parentheses.
List of small abelian groups
The finite abelian groups are easily classified: they are cyclic groups, or direct products thereof; see abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s.
| Order | Group | Subgroups | Properties | Cycle graph Cycle graph (algebra) In group theory, a sub-field of abstract algebra, a group cycle graph illustrates the various cycles of a group and is particularly useful in visualizing the structure of small finite groups... |
|---|---|---|---|---|
| 1 | trivial group Trivial group In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context... = Z1 = S1 = A2 |
- | various properties hold trivially Trivial (mathematics) In mathematics, the adjective trivial is frequently used for objects that have a very simple structure... |
|
| 2 | Z2 = S2 = Dih1 | - | simple, the smallest non-trivial group |  |
| 3 | Z3 = A3 | - | simple |  |
| 4 | Z4 | Z2 |  |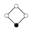
|
| Klein four-group Klein four-group In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2... = = Dih2 |
Z2 (3) | the smallest non-cyclic group |  |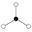
|
| 5 | Z5 | - | simple |  |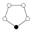
| 6 | Z6 = Z3 × Z2 | Z3 , Z2 |  |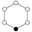
|
| 7 | Z7 | - | simple |  |
| 8 | Z8 | Z4 , Z2 |  |
|
| Z4 × Z2 | , Z4 (2), Z2 (3) |  |
||
| (7) , Z2 (7) | the non-identity elements correspond to the points in the Fano plane Fano plane In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:... , the Z2 × Z2 subgroups to the lines |
 |
||
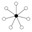| 9 | Z9 | Z3 |  |
|
| Z3 (4) |  |
|||
| 10 | Z10 = Z5 × Z2 | Z5 , Z2 |  |
|
| 11 | Z11 | - | simple |  |
| 12 | Z12 = Z4 × Z3 | Z6 , Z4 , Z3 , Z2 |  |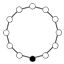
|
| Z6 × Z2 = Z3 × | Z6 (3), Z3, Z2 (3), |  |
||
| 13 | Z13 | - | simple |  |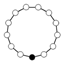
| 14 | Z14 = Z7 × Z2 | Z7 , Z2 |  |
|
| 15 | Z15 = Z5 × Z3 | Z5 , Z3 | multiplication of nimber Nimber In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem... s 1,...,15 |
 |
| 16 | Z16 | Z8 , Z4 , Z2 |  |
|
| Z2 (15) , (35) , (15) | addition of nimbers 0,...,15 |  |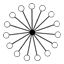
||
| Z4 × | Z2 (7) , Z4 (4) , (7) , , Z4 × Z2 (6) |  |
||
| Z8 × Z2 | Z2 (3) , Z4 (2) , , Z8 (2) , Z4 × Z2 |  |
||
| Z2 (3), Z4 (6) , , Z4 × Z2 (3) |  |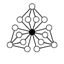
List of small non-abelian groups
| Order | Group | Subgroups | Properties | Cycle Graph Cycle graph (algebra) In group theory, a sub-field of abstract algebra, a group cycle graph illustrates the various cycles of a group and is particularly useful in visualizing the structure of small finite groups... |
|---|---|---|---|---|
| 6 | S3 = Dih3 Dihedral group of order 6 The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 and the symmetric group of degree 3, with notation S3.... | Z3 , Z2 (3) | the smallest non-abelian group |  |
| 8 | Dih4 | Z4, Z22 (2) , Z2 (5) |  | |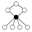
| quaternion group Quaternion group In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication... , Q8 = Dic2 | Z4 (3), Z2 | the smallest Hamiltonian group Hamiltonian group In group theory, a Dedekind group is a group G such that every subgroup of G is normal.All abelian groups are Dedekind groups.A non-abelian Dedekind group is called a Hamiltonian group.... ; smallest group demonstrating that all subgroups may be normal Normal subgroup In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group.... without the group being abelian; the smallest group G demonstrating that for a normal subgroup H the quotient group Quotient group In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation... G/H need not be isomorphic to a subgroup of G |  | |
| 10 | Dih5 | Z5 , Z2 (5) |  | |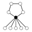
| 12 | Dih6 = Dih3 × Z2 | Z6 , Dih3 (2) , Z22 (3) , Z3 , Z2 (7) |  | |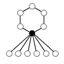
| A4 | Z22 , Z3 (4) , Z2 (3) | smallest group demonstrating that a group need not have a subgroup of every order that divides the group's order: no subgroup of order 6 (See Lagrange's theorem Lagrange's theorem (group theory) Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange.... and the Sylow theorems.) |  | |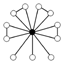
Dic3 = Z3  Z4 | Z2, Z3, Z4 (3), Z6 |  | ||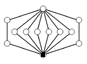
| 14 | Dih7 | Z7, Z2 (7) |  | |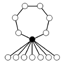
| 16 | Dih8 | Z8, Dih4 (2), Z22 (4), Z4, Z2 (9) |  | |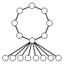
| Dih4 × Z2 | Dih4 (2), Z4 × Z2, Z23 (2), Z22 (11), Z4 (2), Z2 (11) |  | ||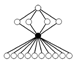
| generalized quaternion group, Q16 = Dic4 |  | |||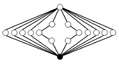
| Q8 × Z2 | Hamiltonian Hamiltonian group In group theory, a Dedekind group is a group G such that every subgroup of G is normal.All abelian groups are Dedekind groups.A non-abelian Dedekind group is called a Hamiltonian group.... |  | ||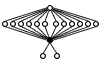
| The order 16 quasidihedral group Quasidihedral group In mathematics, the quasi-dihedral groups and semi-dihedral groups are non-abelian groups of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of nonabelian groups of order 2n which have a cyclic subgroup of index 2... |  | |||
| The order 16 modular group Iwasawa group In mathematics a group is sometimes called an Iwasawa group or M-group or modular group if its lattice of subgroups is modular.Finite modular groups are also called Iwasawa groups, after where they were classified. Both finite and infinite M-groups are presented in textbook form in . Modern... | | |||
Z4  Z4 |  | |||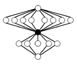
| The group generated by the Pauli matrices | | |||
G4,4 = Z22  Z4 |  |
Small groups library
The group theoretical computer algebra systemComputer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
GAP
GAP computer algebra system
GAP is a computer algebra system for computational discrete algebra with particular emphasis on computational group theory.-History:...
contains the "Small Groups library" which provides access to descriptions of small order groups. The groups are listed up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. At present, the library contains the following groups:
- those of order at most 2000, except for order 1024 ( groups in the library; the ones of order 1024 had to be skipped, as there are an additional nonisomorphic 2-groupsP-groupIn mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
of order 1024.); - those of cubefree order at most 50000 (395 703 groups);
- those of squarefree order;
- those of order
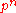for n at most 6 and p prime; - those of order
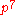for p = 3,5,7,11 (907 489 groups); - those of order qn×p where qn divides 28, 36, 55 or 74 and p is an arbitrary prime which differs from q;
- those whose orders factorise into at most 3 primes.
It contains explicit descriptions of the available groups in computer readable format.
External links
- Particular groups groupprops.subwiki.org, | postscript =. An exhaustive catalog of the 340 groups of order dividing 64 with detailed tables of defining relations, constants, and latticeLattice of subgroupsIn mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....
presentations of each group in the notation the text defines. "Of enduring value to those interested in finite groups" (from the preface).}}