Pure subgroup
Encyclopedia
In mathematics
, especially in the area of algebra
studying the theory of abelian group
s, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.
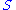of a (typically abelian
) group
is said to be pure if whenever an element of 
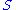has an 
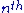root in 
, it necessarily has an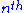 
root in 
.
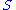's 1923 paper which described conditions for the decomposition of primary abelian group
s as direct sums of cyclic group
s using pure subgroups. The work of Prüfer was complimented nicely by Kulikoff where many results are reproved using pure subgroups systematically. In particular, a nice proof is given that pure subgroups of finite exponent are direct summands. A more complete discussion of pure subgroups, their relation to infinite abelian group theory, and a survey of their literature is given in Irving Kaplansky
's little red book.
Since in a finitely generated Abelian group the torsion subgroup is a direct summand, so one might wish the torsion subgroup was always a direct summand of an Abelian group. Unfortunately it is merely a limit and so is only a pure subgroup. Under certain mild conditions, pure subgroups are direct summands and so one can still recover the desired result under those conditions, as in Kulikoff's paper. This is a typical use of pure subgroups as an intermediate property between an original result on direct summands with finiteness conditions to a full result on direct summands with less restrictive finiteness conditions. Another example of this use is Prüfer's paper which takes the old result that finite torsion Abelian groups are direct sums of cyclic groups and through an intermediate consideration of pure subgroups shows that all torsion Abelian groups of finite exponent are direct sums of cyclic groups.
s were defined in a variety of ways, but eventually settled on the modern definition in terms of tensor products or systems of equations; earlier definitions were usually more direct generalizations such as the single equation used above for n'th roots. Pure injective and pure projective modules follow closely from the ideas of Prüfer's 1923 paper. While pure projective modules have not found as many applications as pure injectives, they are more closely related to the original work: A module is pure projective if it is a direct summand of a direct sum of finitely presented modules. In the case of the integers and Abelian groups, this simple means a direct sum of cyclic groups which was the original motivation for the study of pure subgroups in Prüfer's 1923 paper.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
studying the theory of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.
Definition
A subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
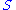of a (typically abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
) group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
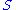is said to be pure if whenever an element of has an 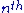root in , it necessarily has an 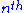root in 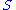.Origins
Pure subgroups are also called isolated subgroups or serving subgroups and were first investigated in PrüferHeinz Prüfer
Ernst Paul Heinz Prüfer was a German mathematician, who worked on abelian groups, algebraic numbers, knot theory and Sturm-Liouville theory. His advisor was Issai Schur.- See also :* Prüfer manifold...
's 1923 paper which described conditions for the decomposition of primary abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s as direct sums of cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s using pure subgroups. The work of Prüfer was complimented nicely by Kulikoff where many results are reproved using pure subgroups systematically. In particular, a nice proof is given that pure subgroups of finite exponent are direct summands. A more complete discussion of pure subgroups, their relation to infinite abelian group theory, and a survey of their literature is given in Irving Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
's little red book.
Examples
- Every direct summand of a group is a pure subgroup
- Every pure subgroup of a pure subgroup is pure.
- A divisibleDivisible groupIn mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
subgroup of an Abelian group is pure. - If the quotient group is torsion-free, the subgroup is pure.
- The torsion subgroup of an Abelian group is pure.
- The union of pure subgroups is a pure subgroup.
Since in a finitely generated Abelian group the torsion subgroup is a direct summand, so one might wish the torsion subgroup was always a direct summand of an Abelian group. Unfortunately it is merely a limit and so is only a pure subgroup. Under certain mild conditions, pure subgroups are direct summands and so one can still recover the desired result under those conditions, as in Kulikoff's paper. This is a typical use of pure subgroups as an intermediate property between an original result on direct summands with finiteness conditions to a full result on direct summands with less restrictive finiteness conditions. Another example of this use is Prüfer's paper which takes the old result that finite torsion Abelian groups are direct sums of cyclic groups and through an intermediate consideration of pure subgroups shows that all torsion Abelian groups of finite exponent are direct sums of cyclic groups.
Generalizations
Pure subgroups were generalized in several ways in the theory of abelian groups and modules. Pure submodulePure submodule
In mathematics, especially in the field of module theory, the concept of pure submodule provides a generalization of direct summand, a type of particularly well-behaved piece of a module. Pure modules are complementary to flat modules and generalize Prüfer's notion of pure subgroups...
s were defined in a variety of ways, but eventually settled on the modern definition in terms of tensor products or systems of equations; earlier definitions were usually more direct generalizations such as the single equation used above for n'th roots. Pure injective and pure projective modules follow closely from the ideas of Prüfer's 1923 paper. While pure projective modules have not found as many applications as pure injectives, they are more closely related to the original work: A module is pure projective if it is a direct summand of a direct sum of finitely presented modules. In the case of the integers and Abelian groups, this simple means a direct sum of cyclic groups which was the original motivation for the study of pure subgroups in Prüfer's 1923 paper.