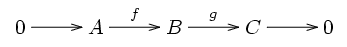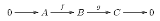
Pure submodule
Encyclopedia
In mathematics
, especially in the field of module theory, the concept of pure submodule provides a generalization of direct summand, a type of particularly well-behaved piece of a module
. Pure modules are complementary to flat module
s and generalize Prüfer's notion of pure subgroup
s. While flat modules are those modules which leave short exact sequences exact after tensoring
, a pure submodule defines a short exact sequence that remains exact after tensoring with any module. Similarly a flat module is a direct limit
of projective module
s, and a pure submodule defines a short exact sequence which is a direct limit of split exact sequences, each defined by a direct summand.
, and let M, P be module
s over R. If i: P → M is injective then P is a pure submodule of M if, for any R-module X, the natural induced map on tensor product
s i⊗idX:P⊗X → M⊗X is injective.
Analogously, a short exact sequence
of R-modules is pure exact if the sequence stays exact when tensored with any R-module X. This is equivalent to saying that f(A) is a pure submodule of B.
Purity can also be expressed element-wise; it is really a statement about the solvability of certain systems of linear equations. Specifically, P is pure in M if and only if the following condition holds: for any m-by-n matrix
(aij) with entries in R, and any set y1,...,ym of elements of P, if there exist elements x1,...,xn in M such that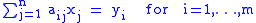
then there also exist elements x1',..., xn' in P such that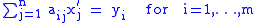
Suppose
is a short exact sequence of R modules, then:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the field of module theory, the concept of pure submodule provides a generalization of direct summand, a type of particularly well-behaved piece of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Pure modules are complementary to flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
s and generalize Prüfer's notion of pure subgroup
Pure subgroup
In mathematics, especially in the area of algebra studying the theory of abelian groups, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.-Definition:...
s. While flat modules are those modules which leave short exact sequences exact after tensoring
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, a pure submodule defines a short exact sequence that remains exact after tensoring with any module. Similarly a flat module is a direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s, and a pure submodule defines a short exact sequence which is a direct limit of split exact sequences, each defined by a direct summand.
Definition
Let R be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, and let M, P be module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over R. If i: P → M is injective then P is a pure submodule of M if, for any R-module X, the natural induced map on tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s i⊗idX:P⊗X → M⊗X is injective.
Analogously, a short exact sequence
of R-modules is pure exact if the sequence stays exact when tensored with any R-module X. This is equivalent to saying that f(A) is a pure submodule of B.
Purity can also be expressed element-wise; it is really a statement about the solvability of certain systems of linear equations. Specifically, P is pure in M if and only if the following condition holds: for any m-by-n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(aij) with entries in R, and any set y1,...,ym of elements of P, if there exist elements x1,...,xn in M such that
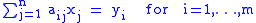
then there also exist elements x1',..., xn' in P such that
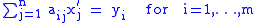
Examples
- Every direct summand of M is pure in M. Consequently, every subspaceSubspace-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is pure.
Suppose
is a short exact sequence of R modules, then:
- C is a flat moduleFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
if and only if the exact sequence is pure exact for every A and B. From this we can deduce that over a von Neumann regular ringVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
, every submodule of every R-module is pure. This is because every module over a von Neumann regular ring is flat. The converse is also true. - Suppose B is flat. Then the sequence is pure exact if and only if C is flat. From this one can deduce that pure submodules of flat modules are flat.
- Suppose C is flat. Then B is flat if and only if A is flat.