
Von Neumann regular ring
Encyclopedia
In mathematics
, a von Neumann regular ring is a ring
R such that for every a in R there exists an x in R with
One may think of x as a "weak inverse" of a. In general x is not uniquely determined by a.
Von Neumann regular rings were introduced by under the name of "regular rings", during his study of von Neumann algebra
s and continuous geometry
.
The regular ring
s and regular local ring
s of commutative algebra
are unrelated to von Neumann regular rings.
(and every skew field) is von Neumann regular: for a≠0 we can take x = a -1. An integral domain is von Neumann regular if and only if it is a field.
Another example of a von Neumann regular ring is the ring Mn(K) of n-by-n square matrices with entries from some field K. If r is the rank of A∈Mn(K), then there exist invertible matrices U and V such that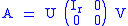
(where Ir is the r-by-r identity matrix
). If we set X = V -1U -1, then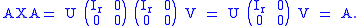
The ring of affiliated operator
s of a finite von Neumann algebra
is von Neumann regular.
A Boolean ring
is a ring in which every element satisfies a2 = a. Every Boolean ring is von Neumann regular.
The corresponding statements for right modules are also equivalent to R being von Neumann regular.
In a commutative von Neumann regular ring,
for each element x there is a unique element y such that xyx=x and yxy=y, so there is a canonical way to choose the "weak inverse" of x.
The following statements are equivalent for the commutative ring R:
Also, the following are equivalent: for a commutative ring A
Every semisimple ring is von Neumann regular, and a left (or right) Noetherian
von Neumann regular ring is semisimple. Every von Neumann regular ring has Jacobson radical
{0} and is thus semiprimitive
(also called "Jacobson semi-simple").
Generalizing the above example, suppose S is some ring and M is an S-module such that every submodule of M is a direct summand of M (such modules M are called semisimple
). Then the endomorphism ring
EndS(M) is von Neumann regular. In particular, every semisimple ring is von Neumann regular.
s.
A ring R is called unit regular if for every a in R, there is a unit u in R such that a=aua. Every semisimple ring ring is unit regular, and unit regular rings are directly finite rings. An ordinary von Neumann regular ring need not be directly finite.
A ring R is called strongly von Neumann regular if for every a in R, there is some x in R with a = aax. The condition is left-right symmetric. Strongly von Neumann regular rings are unit regular. Every strongly von Neumann regular ring is a subdirect product
of division ring
s. In some sense, this more closely mimics the properties of commutative von Neumann regular rings, which are subdirect products of fields. Of course for commutative rings, von Neumann regular and strongly von Neumann regular are equivalent. In general, the following are equivalent for a ring R:
Generalizations of von Neumann regular rings include π-regular rings, left/right semihereditary rings, left/right nonsingular rings and semiprimitive ring
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a von Neumann regular ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R such that for every a in R there exists an x in R with
- a = axa.
One may think of x as a "weak inverse" of a. In general x is not uniquely determined by a.
Von Neumann regular rings were introduced by under the name of "regular rings", during his study of von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s and continuous geometry
Continuous geometry
In mathematics, continuous geometry is an analogue of complex projective geometry introduced by , where instead of the dimension of a subspace being in a discrete set 0, 1, ..., n, it can be an element of the unit interval [0,1]...
.
The regular ring
Regular ring
In commutative algebra, a regular ring is a commutative noetherian ring, such that the localization at every prime ideal is a regular local ring: that is, every such localization has the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension.Jean-Pierre...
s and regular local ring
Regular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
s of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
are unrelated to von Neumann regular rings.
Examples
Every fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(and every skew field) is von Neumann regular: for a≠0 we can take x = a -1. An integral domain is von Neumann regular if and only if it is a field.
Another example of a von Neumann regular ring is the ring Mn(K) of n-by-n square matrices with entries from some field K. If r is the rank of A∈Mn(K), then there exist invertible matrices U and V such that
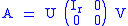
(where Ir is the r-by-r identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
). If we set X = V -1U -1, then
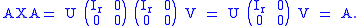
The ring of affiliated operator
Affiliated operator
In mathematics, affiliated operators were introduced by Murray and von Neumann in the theory of von Neumann algebras as a technique for using unbounded operators to study modules generated by a single vector...
s of a finite von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
is von Neumann regular.
A Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
is a ring in which every element satisfies a2 = a. Every Boolean ring is von Neumann regular.
Facts
The following statements are equivalent for the ring R:- R is von Neumann regular
- every principalPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
left ideal is generated by an idempotent - every finitely generated left ideal is generated by an idempotent
- every principal left ideal is a direct summand of the left R-module R
- every finitely generated left ideal is a direct summand of the left R-module R
- every finitely generated submodule of a projectiveProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
left R-module P is a direct summand of P - every left R-module is flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
: this is also known as R being absolutely flat, or R having weak dimension 0. - every short exact sequence of left R-modules is pure exact
The corresponding statements for right modules are also equivalent to R being von Neumann regular.
In a commutative von Neumann regular ring,
for each element x there is a unique element y such that xyx=x and yxy=y, so there is a canonical way to choose the "weak inverse" of x.
The following statements are equivalent for the commutative ring R:
- R is von Neumann regular
- R has Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
0 and is reducedReduced ringIn ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0... - Every localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of R at a maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
is a field - R is a subring of a product of fields closed under taking "weak inverses" of x∈R (the unique element y such that xyx=x and yxy=y).
Also, the following are equivalent: for a commutative ring A
-
 is von Neumann regular.
is von Neumann regular. - The spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of R is Hausdorff (with respect to Zariski topology). - The constructible topology and Zariski topology for
 coincide.
coincide.
Every semisimple ring is von Neumann regular, and a left (or right) Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
von Neumann regular ring is semisimple. Every von Neumann regular ring has Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
{0} and is thus semiprimitive
Semiprimitive ring
In mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
(also called "Jacobson semi-simple").
Generalizing the above example, suppose S is some ring and M is an S-module such that every submodule of M is a direct summand of M (such modules M are called semisimple
Semisimple
In mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
). Then the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
EndS(M) is von Neumann regular. In particular, every semisimple ring is von Neumann regular.
Generalizations and specializations
Special types of von Neumann regular rings include unit regular rings and strongly von Neumann regular rings and rank ringRank ring
In mathematics, a rank ring is a ring with a real-valued rank function behaving like the rank of an endomorphism. introduced rank rings in his work on continuous geometry, and showed that the ring associated to a continuous geometry is a rank ring....
s.
A ring R is called unit regular if for every a in R, there is a unit u in R such that a=aua. Every semisimple ring ring is unit regular, and unit regular rings are directly finite rings. An ordinary von Neumann regular ring need not be directly finite.
A ring R is called strongly von Neumann regular if for every a in R, there is some x in R with a = aax. The condition is left-right symmetric. Strongly von Neumann regular rings are unit regular. Every strongly von Neumann regular ring is a subdirect product
Subdirect product
In mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however necessarily being the whole direct product...
of division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s. In some sense, this more closely mimics the properties of commutative von Neumann regular rings, which are subdirect products of fields. Of course for commutative rings, von Neumann regular and strongly von Neumann regular are equivalent. In general, the following are equivalent for a ring R:
- R is strongly von Neumann regular
- R is von Neumann regular and reducedReduced ringIn ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
- R is von Neumann regular and every idempotent in R is central
- Every principal left ideal of R is generated by a central idempotent
Generalizations of von Neumann regular rings include π-regular rings, left/right semihereditary rings, left/right nonsingular rings and semiprimitive ring
Semiprimitive ring
In mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
s.

