Constructible topology
Encyclopedia
In commutative algebra
, the constructible topology on the spectrum
of a commutative ring
is a topology
where each closed set is the image of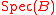
in 
for some algebra
B over A. An important feature of this construction is that the map
is a closed map with respect to the constructible topology.
With respect to this topology,
is a compact, Hausdorff
, and totally disconnected topological space
. In general the constructible topology is a finer topology than the Zariski topology
, but the two topologies will coincide if and only if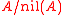
is a von Neumann regular ring
, where
is the nilradical of A.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the constructible topology on the spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
is a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
where each closed set is the image of
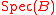in for some algebraAlgebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
B over A. An important feature of this construction is that the map
is a closed map with respect to the constructible topology.With respect to this topology,
is a compact, HausdorffHausdorff
Hausdorff may refer to:* A Hausdorff space, when used as an adjective, as in "the real line is Hausdorff."* Felix Hausdorff , the German mathematician after whom Hausdorff spaces are named...
, and totally disconnected topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. In general the constructible topology is a finer topology than the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, but the two topologies will coincide if and only if
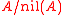is a von Neumann regular ringVon Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
, where
is the nilradical of A.