In the branch of mathematics

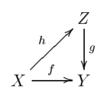
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 called category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

, given a morphism

Morphism

In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

 f from an object X to an object Y, and a morphism g from an object Z to Y, a lift (or lifting) of f to Z is a morphism h from X to Z such that gh = f.

A basic example in topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 is lifting a path

Path (topology)

In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...

 in one space to a path in a covering space. Consider, for instance, mapping opposite points on a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 to the same point, a continuous map from the sphere covering the projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

. A path in the projective plane is a continuous map from the unit interval, [0,1]. We can lift such a path to the sphere by choosing one of the two sphere points mapping to the first point on the path, then maintain continuity. In this case, each of the two starting points forces a unique path on the sphere, the lift of the path in the projective plane. Thus in the category of topological spaces with continuous maps as morphisms, we have

Lifts are ubiquitous; for example, the definition of fibration

Fibration

In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...

s (see homotopy lifting property

Homotopy lifting property

In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...

) and the valuative criteria of separated and proper map

Proper map

In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...

s of schemes

Scheme (mathematics)

In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...

are formulated in terms of existence and (in the last case) unicity of certain lifts.