
Burnside ring
Encyclopedia
In mathematics
, the Burnside ring of a finite group
is an algebraic construction that encodes the different ways the group can act
on finite sets. The ideas were introduced by William Burnside
at the end of the nineteenth century, but the algebraic ring structure
is a more recent development, due to Solomon (1967).
G, the elements of its Burnside ring Ω(G) are the formal differences of isomorphism classes of finite G-sets
. For the ring structure
, addition is given by disjoint union
of G-sets, and multiplication by their Cartesian product
.
The Burnside ring is a free Z-module
, whose generators are the (isomorphism classes of) orbit types
of G.
If G acts on a finite set X, then one can write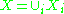 (disjoint union), where each Xi is a single G-orbit. Choosing any element xi in Xi creates an isomorphism G/Gi → Xi, where Gi is the stabilizer (isotropy) subgroup of G at xi. A different choice of representative yi in Xi gives a conjugate subgroup to Gi as stabilizer. This shows that the generators of Ω(G) as a Z-module are the orbits G/H as H ranges over conjugacy classes of subgroups of G.
(disjoint union), where each Xi is a single G-orbit. Choosing any element xi in Xi creates an isomorphism G/Gi → Xi, where Gi is the stabilizer (isotropy) subgroup of G at xi. A different choice of representative yi in Xi gives a conjugate subgroup to Gi as stabilizer. This shows that the generators of Ω(G) as a Z-module are the orbits G/H as H ranges over conjugacy classes of subgroups of G.
In other words, a typical element of Ω(G) is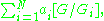
where ai in Z and G1, G2, ..., GN are representatives of the conjugacy classes of subgroups of G.
simplifies working with group representation
s, marks simplify working with permutation representations and the Burnside ring.
If G acts on X, and H ≤ G (H is a subgroup
of G), then the mark of H on X is the number of elements of X that are fixed by every element of H: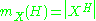 , where
, where
If H and K are conjugate subgroups, then mX(H) = mX(K) for any finite G-set X; indeed, if K = gHg−1 then XK = g · XH.
It is also easy to see that for each H ≤ G, the map Ω(G) → Z : X ↦ mX(H) is a homomorphism. This means that to know the marks of G, it is sufficient to evaluate them on the generators of Ω(G), viz. the orbits G/H.
For each pair of subgroups H,K ≤ G define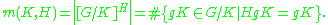
This is mX(H) for X = G/K. The condition HgK = gK is equivalent to g−1Hg ≤ K, so if H is not conjugate to a subgroup of K then m(K, H) = 0.
To record all possible marks, one forms a table, Burnside's Table of Marks, as follows: Let G1 (= trivial subgroup), G2, ..., GN = G be representatives of the N conjugacy classes of subgroups of G, ordered in such a way that whenever Gi is conjugate to a subgroup of Gj, then i ≤ j. Now define the N × N table (square matrix) whose (i, j)th entry is m(Gi, Gj). This matrix is lower triangular, and the elements on the diagonal are non-zero so it is invertible.
It follows that if X is a G-set, and u its row vector of marks, so ui = mX(Gi), then X decomposes as a disjoint union
of ai copies of the orbit of type Gi, where the vector a satisfies,
where M is the matrix of the table of marks. This theorem is due to .
The table of marks for the symmetric group S3 on 3 letters:
The dots in the two tables are all zeros, merely emphasizing the fact that the tables are lower-triangular.
(Some authors use the transpose of the table, but this is how Burnside defined it originally.)
The fact that the last row is all 1s is because [G/G] is a single point. The diagonal terms are m(H, H) = | NG(H)/H |.
The ring structure of Ω(G) can be deduced from these tables: the generators of the ring (as a Z-module) are the rows of the table, and the product of two generators has mark given by the product of the marks (so component-wise multiplication of row vectors), which can then be decomposed as a linear combination
of all the rows. For example, with S3,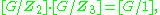
as (3, 1, 0, 0).(2, 0, 2, 0) = (6, 0, 0, 0).
V = VX, which is the vector space with the elements of X as the basis (using any specified field). An action of a finite group G on X induces a linear action on V, called a permutation representation
. The set of all finite dimensional representations of G has the structure of a ring, the representation ring
, denoted R(G).
For a given G-set X, the character
of the associated representation is

where is the cyclic group generated by g.
The resulting map
taking a G-set to the corresponding representation is in general neither injective nor surjective.
The simplest example showing that β is not in general injective is for G = S3 (see table above), and is given by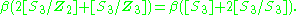
s is described in .
The Segal conjecture
relates the Burnside ring to homotopy
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Burnside ring of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is an algebraic construction that encodes the different ways the group can act
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on finite sets. The ideas were introduced by William Burnside
William Burnside
William Burnside was an English mathematician. He is known mostly as an early contributor to the theory of finite groups....
at the end of the nineteenth century, but the algebraic ring structure
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is a more recent development, due to Solomon (1967).
Formal definition
Given a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G, the elements of its Burnside ring Ω(G) are the formal differences of isomorphism classes of finite G-sets
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. For the ring structure
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, addition is given by disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of G-sets, and multiplication by their Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
.
The Burnside ring is a free Z-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, whose generators are the (isomorphism classes of) orbit types
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G.
If G acts on a finite set X, then one can write
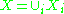 (disjoint union), where each Xi is a single G-orbit. Choosing any element xi in Xi creates an isomorphism G/Gi → Xi, where Gi is the stabilizer (isotropy) subgroup of G at xi. A different choice of representative yi in Xi gives a conjugate subgroup to Gi as stabilizer. This shows that the generators of Ω(G) as a Z-module are the orbits G/H as H ranges over conjugacy classes of subgroups of G.
(disjoint union), where each Xi is a single G-orbit. Choosing any element xi in Xi creates an isomorphism G/Gi → Xi, where Gi is the stabilizer (isotropy) subgroup of G at xi. A different choice of representative yi in Xi gives a conjugate subgroup to Gi as stabilizer. This shows that the generators of Ω(G) as a Z-module are the orbits G/H as H ranges over conjugacy classes of subgroups of G.In other words, a typical element of Ω(G) is
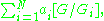
where ai in Z and G1, G2, ..., GN are representatives of the conjugacy classes of subgroups of G.
Marks
Much like character theoryCharacter theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
simplifies working with group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, marks simplify working with permutation representations and the Burnside ring.
If G acts on X, and H ≤ G (H is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G), then the mark of H on X is the number of elements of X that are fixed by every element of H:
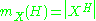 , where
, where
If H and K are conjugate subgroups, then mX(H) = mX(K) for any finite G-set X; indeed, if K = gHg−1 then XK = g · XH.
It is also easy to see that for each H ≤ G, the map Ω(G) → Z : X ↦ mX(H) is a homomorphism. This means that to know the marks of G, it is sufficient to evaluate them on the generators of Ω(G), viz. the orbits G/H.
For each pair of subgroups H,K ≤ G define
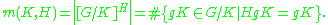
This is mX(H) for X = G/K. The condition HgK = gK is equivalent to g−1Hg ≤ K, so if H is not conjugate to a subgroup of K then m(K, H) = 0.
To record all possible marks, one forms a table, Burnside's Table of Marks, as follows: Let G1 (= trivial subgroup), G2, ..., GN = G be representatives of the N conjugacy classes of subgroups of G, ordered in such a way that whenever Gi is conjugate to a subgroup of Gj, then i ≤ j. Now define the N × N table (square matrix) whose (i, j)th entry is m(Gi, Gj). This matrix is lower triangular, and the elements on the diagonal are non-zero so it is invertible.
It follows that if X is a G-set, and u its row vector of marks, so ui = mX(Gi), then X decomposes as a disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of ai copies of the orbit of type Gi, where the vector a satisfies,
- aM = u,
where M is the matrix of the table of marks. This theorem is due to .
Examples
The table of marks for the cyclic group of order 6:| Z6 | 1 | Z2 | Z3 | Z6 |
| Z6 / 1 | 6 | . | . | . |
| Z6 / Z2 | 3 | 3 | . | . |
| Z6 / Z3 | 2 | 0 | 2 | . |
| Z6 / Z6 | 1 | 1 | 1 | 1 |
The table of marks for the symmetric group S3 on 3 letters:
| S3 | 1 | Z2 | Z3 | S3 |
| S3 / 1 | 6 | . | . | . |
| S3 / Z2 | 3 | 1 | . | . |
| S3 / Z3 | 2 | 0 | 2 | . |
| S3 / S3 | 1 | 1 | 1 | 1 |
The dots in the two tables are all zeros, merely emphasizing the fact that the tables are lower-triangular.
(Some authors use the transpose of the table, but this is how Burnside defined it originally.)
The fact that the last row is all 1s is because [G/G] is a single point. The diagonal terms are m(H, H) = | NG(H)/H |.
The ring structure of Ω(G) can be deduced from these tables: the generators of the ring (as a Z-module) are the rows of the table, and the product of two generators has mark given by the product of the marks (so component-wise multiplication of row vectors), which can then be decomposed as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of all the rows. For example, with S3,
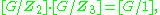
as (3, 1, 0, 0).(2, 0, 2, 0) = (6, 0, 0, 0).
Permutation representations
Associated to any finite set X is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V = VX, which is the vector space with the elements of X as the basis (using any specified field). An action of a finite group G on X induces a linear action on V, called a permutation representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
. The set of all finite dimensional representations of G has the structure of a ring, the representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
, denoted R(G).
For a given G-set X, the character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of the associated representation is

where
The resulting map

taking a G-set to the corresponding representation is in general neither injective nor surjective.
The simplest example showing that β is not in general injective is for G = S3 (see table above), and is given by
Extensions
The Burnside ring for compact groupCompact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s is described in .
The Segal conjecture
Segal conjecture
Segal's Burnside ring conjecture, or, more briefly, the Segal conjecture, is a theorem in homotopy theory, a branch of mathematics. The theorem relates the Burnside ring of a finite group G to the stable cohomotopy of the classifying space BG. The conjecture was made by Graeme Segal and proved by...
relates the Burnside ring to homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
.

