
Segal conjecture
Encyclopedia
Segal's Burnside ring conjecture, or, more briefly, the Segal conjecture, is a theorem
in homotopy theory, a branch of mathematics
. The theorem relates the Burnside ring
of a finite group
G to the stable cohomotopy of the classifying space
BG. The conjecture was made by Graeme Segal
and proved by Gunnar Carlsson. , this statement is still commonly referred to as the Segal conjecture, even though it now has the status of a theorem.
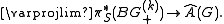
Here, lim denotes the inverse limit
, πS* denotes the stable cohomotopy ring, B denotes the classifying space, the superscript k denotes the k-skeleton, and the superscript + denotes the addition of a disjoint basepoint. On the right-hand side, the hat denotes the completion of the Burnside ring with respect to its augmentation ideal
.
as a Grothendieck group
. More precisely, let M(G) be the commutative monoid
of isomorphism classes of finite G-sets, with addition the disjoint union of G-sets and identity element the empty set (which is a G-set in a unique way). Then A(G), the Grothendieck group of M(G), is an abelian group. It is in fact a free
abelian group with basis elements represented by the G-sets G/H, where H varies over the subgroups of G. (Note that H is not assumed here to be a normal subgroup of G, for while G/H is not a group in this case, it is still a G-set.) The ring
structure on A(G) is induced by the direct product of G-sets; the multiplicative identity is the (isomorphism class of any) one-point set, which becomes a G-set in a unique way.
The Burnside ring is the analogue of the representation ring
in the category of finite sets, as opposed to the category of finite-dimensional vector space
s over a field
(see motivation below). It has proven to be an important tool in the representation theory
of finite groups.
G admitting the structure of a CW-complex, one may consider the category of principal G-bundles
. One can define a functor
from the category of CW-complexes to the category of sets by assigning to each CW-complex X the set of principal G-bundles on X. This functor descends to a functor on the homotopy category of CW-complexes, and it is natural to ask whether the functor so obtained is representable
. The answer is affirmative, and the representing object is called the classifying space of the group G and typically denoted BG. If we restrict our attention to the homotopy category of CW-complexes, then BG is unique. Any CW-complex that is homotopy equivalent to BG is called a model for BG.
For example, if G is the group of order 2, then a model for BG is infinite-dimensional real projective space. It can be shown that if G is finite, then any CW-complex modelling BG has cells of arbitrarily large dimension. On the other hand, if G = Z, the integers, then the classifying space BG is homotopy equivalent to the circle S1.
, which is denoted KU*. Segal was inspired to make his conjecture after Michael Atiyah
proved the existence of an isomorphism
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in homotopy theory, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. The theorem relates the Burnside ring
Burnside ring
In mathematics, the Burnside ring of a finite group is an algebraic construction that encodes the different ways the group can act on finite sets...
of a finite group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G to the stable cohomotopy of the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG. The conjecture was made by Graeme Segal
Graeme Segal
Graeme Bryce Segal is a British mathematician, and professor at the University of Oxford.Segal was educated at the University of Sydney, where he received his BSc degree in 1961. He went on to receive his D.Phil...
and proved by Gunnar Carlsson. , this statement is still commonly referred to as the Segal conjecture, even though it now has the status of a theorem.
Statement of the theorem
The Segal conjecture has several different formulations, not all of which are equivalent. Here is a weak form: there exists, for every finite group G, an isomorphism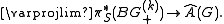
Here, lim denotes the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
, πS* denotes the stable cohomotopy ring, B denotes the classifying space, the superscript k denotes the k-skeleton, and the superscript + denotes the addition of a disjoint basepoint. On the right-hand side, the hat denotes the completion of the Burnside ring with respect to its augmentation ideal
Augmentation ideal
In algebra, an augmentation ideal is an ideal that can be defined in any group ring. If G is a group and R a commutative ring, there is a ring homomorphism \varepsilon, called the augmentation map, from the group ring...
.
The Burnside ring
The Burnside ring of a finite group G is constructed from the category of finite G-setsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
as a Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
. More precisely, let M(G) be the commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of isomorphism classes of finite G-sets, with addition the disjoint union of G-sets and identity element the empty set (which is a G-set in a unique way). Then A(G), the Grothendieck group of M(G), is an abelian group. It is in fact a free
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
abelian group with basis elements represented by the G-sets G/H, where H varies over the subgroups of G. (Note that H is not assumed here to be a normal subgroup of G, for while G/H is not a group in this case, it is still a G-set.) The ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure on A(G) is induced by the direct product of G-sets; the multiplicative identity is the (isomorphism class of any) one-point set, which becomes a G-set in a unique way.
The Burnside ring is the analogue of the representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
in the category of finite sets, as opposed to the category of finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(see motivation below). It has proven to be an important tool in the representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of finite groups.
The classifying space
For any topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G admitting the structure of a CW-complex, one may consider the category of principal G-bundles
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. One can define a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of CW-complexes to the category of sets by assigning to each CW-complex X the set of principal G-bundles on X. This functor descends to a functor on the homotopy category of CW-complexes, and it is natural to ask whether the functor so obtained is representable
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
. The answer is affirmative, and the representing object is called the classifying space of the group G and typically denoted BG. If we restrict our attention to the homotopy category of CW-complexes, then BG is unique. Any CW-complex that is homotopy equivalent to BG is called a model for BG.
For example, if G is the group of order 2, then a model for BG is infinite-dimensional real projective space. It can be shown that if G is finite, then any CW-complex modelling BG has cells of arbitrarily large dimension. On the other hand, if G = Z, the integers, then the classifying space BG is homotopy equivalent to the circle S1.
Motivation and interpretation
The content of the theorem becomes somewhat clearer if it is placed in its historical context. In the theory of representations of finite groups, one can form an object R[G] called the representation ring in a way entirely analogous to the construction of the Burnside ring outlined above. The stable cohomotopy is in a sense the natural analog to complex K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, which is denoted KU*. Segal was inspired to make his conjecture after Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
proved the existence of an isomorphism


