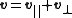In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

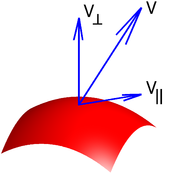
, given a vector at a point on a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

, that vector can be decomposed uniquely as a sum of two vectors, one tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 to the curve, called the tangential component of the vector, and another one perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

 to the curve, called the normal component of the vector. Similarly a vector at a point on a surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

 can be broken down the same way.

More generally, given a submanifold

Submanifold

In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...

 N of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 M, and a vector in the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 to M at a point of N, it can be decomposed into the component tangent to N and the component normal to N.

Surface

More formally, let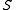 be a surface, and be a point on the surface. Let be a vector at Then one can write uniquely as a sum

where the first vector in the sum is the tangential component and the second one is the normal component. It follows immediately that these two vectors are perpendicular to each other.

To calculate the tangential and normal components, consider a unit normal

Surface normal

A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...

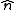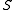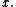 to the surface, that is, a unit vector  perpendicular to at Then,


and thus


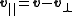
where "" denotes the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

. Another formula for the tangential component is


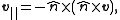
where "" denotes the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

.

Note that these formulas do not depend on the particular unit normal 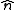used (there exist two unit normals to any surface at a given point, pointing in opposite directions, so one of the unit normals is the negative of the other one).

Submanifold

More generally, given a submanifold

Submanifold

In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...

 N of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 M and
a point 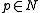, we get a short exact sequence
involving the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

s:
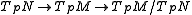
The quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

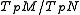  is a generalized space of normal vectors.

If M is a Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

, the above sequence splits, and the tangent space of M at p decomposes as a direct sum of the component tangent to N and the component normal to N:
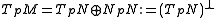
Thus every tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

  splits as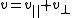
,
where 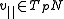and .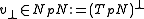

Computations

Suppose N is given by non-degenerate equations.

If N is given explicitly, via parametric equation

Parametric equation

In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....

s (such as a parametric curve), then the derivative gives a spanning set for the tangent bundle (it's a basis if and only if the parametrization is an immersion).

If N is given implicitly (as in the above description of a surface, or more generally as a hypersurface

Hypersurface

In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...

) as a level set

Level set

In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....

 or intersection of level surfaces for 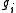, then the gradients of 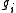span the normal space.

In both cases, we can again compute using the dot product; the cross product is special to 3 dimensions though.

Applications

• Lagrange multipliers
  Lagrange multipliers
  In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
  
   : constrained critical points
  Critical point (mathematics)
  In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
  
   are where the tangential component of the total derivative
  Total derivative
  In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
  
   vanish.
• Surface normal
  Surface normal
  A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...