
Truncated cubic honeycomb
Encyclopedia
 |
|
| Type | Uniform honeycomb Convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;... |
| Schläfli symbol | t0,1{4,3,4} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| Cell type | 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... , {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
| Face type | {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... , {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... , {8} |
| Cells/edge | (3.8.8)4 {3,4}.(3.8.8)2 |
| Faces/edge | {8}4 {3}2.{8} |
| Cells/vertex | 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... (4) {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... (1) |
| Faces/vertex | {8}4+{3}4 |
| Edges/vertex | 5 |
| Euler characteristic Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
0 |
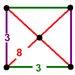
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
 , [4,3,4] , [4,3,4] |
| Dual | Hexakis cubic honeycomb |
| Properties | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... |
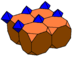
The truncated cubic honeycomb is a uniform space-filling tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
(or honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) in Euclidean 3-space. It is composed of truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
s and octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
in a ratio of 1:1.

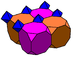
Symmetry
There is a second uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s by reflectional symmetry of the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, the second seen with alternately colored truncated cubic cells.
| Construction | Truncated cubic honeycomb | Bicantellated alternate cubic |
|---|---|---|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
[4,3,4],  |
[4,31,1],  |
| Coloring |  |
 |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
 |
 |

