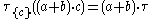Algebra of Communicating Processes
Encyclopedia
The Algebra of Communicating Processes (ACP) is an algebraic
approach to reasoning about concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras or process calculi. ACP was initially developed by Jan Bergstra
and Jan Willem Klop
in 1982, as part of an effort to investigate the solutions of unguarded recursive equations. More so than the other seminal process calculi (CCS
and CSP
), the development of ACP focused on the algebra
of processes, and sought to create an abstract, generalized axiomatic system for processes, and in fact the term process algebra was coined during the research that led to ACP.
. This algebra provides a way to describe systems in terms of algebraic process expressions that define compositions of other processes, or of certain primitive elements.
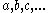 ) as its primitives. Some actions have special meaning, such as the action
) as its primitives. Some actions have special meaning, such as the action  , which represents deadlock
, which represents deadlock
or stagnation, and the action , which represents a silent action (abstracted actions that have no specific identity).
, which represents a silent action (abstracted actions that have no specific identity).
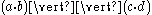

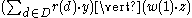
 (ACP with abstraction).
(ACP with abstraction).

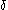
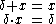
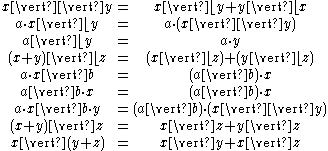
When the communications operator is applied to actions alone, rather than processes, it is interpreted as a binary function from actions to actions,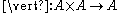 . The definition of this function defines the possible interactions between processes — those pairs of actions that do not constitute interactions are mapped to the deadlock action,
. The definition of this function defines the possible interactions between processes — those pairs of actions that do not constitute interactions are mapped to the deadlock action, 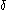 , while permitted interaction pairs are mapped to corresponding single actions representing the occurrence of an interaction. For example, the communications function might specify that
, while permitted interaction pairs are mapped to corresponding single actions representing the occurrence of an interaction. For example, the communications function might specify that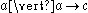
which indicates that a successful interaction will be reduced to the action
will be reduced to the action  . ACP also includes an encapsulation operator,
. ACP also includes an encapsulation operator, 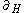 for some
for some 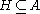 , which is used to convert unsuccessful communication attempts (i.e. elements of
, which is used to convert unsuccessful communication attempts (i.e. elements of  that have not been reduced via the communication function) to the deadlock action. The axioms associated with the communications function and encapsulation operator are
that have not been reduced via the communication function) to the deadlock action. The axioms associated with the communications function and encapsulation operator are

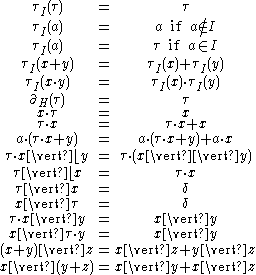
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
approach to reasoning about concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras or process calculi. ACP was initially developed by Jan Bergstra
Jan Bergstra
Jan A. Bergstra is a Dutch computer scientist. His work has focussed on logic and the theoretical foundations of software engineering, especially on formal methods for system design...
and Jan Willem Klop
Jan Willem Klop
Jan Willem Klop is a professor of applied logic at Vrije Universiteit in Amsterdam. He holds a Ph.D. in mathematical logic from Utrecht University. Klop is known for his work on the Algebra of Communicating Processes, co-author of TeReSe and his fixed point combinatorwhere- External links :*...
in 1982, as part of an effort to investigate the solutions of unguarded recursive equations. More so than the other seminal process calculi (CCS
Calculus of Communicating Systems
The Calculus of Communicating Systems is a process calculus introduced by Robin Milner around 1980 and the title of a book describing the calculus. Its actions model indivisible communications between exactly two participants. The formal language includes primitives for describing parallel...
and CSP
Communicating sequential processes
In computer science, Communicating Sequential Processes is a formal language for describing patterns of interaction in concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras, or process calculi...
), the development of ACP focused on the algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
of processes, and sought to create an abstract, generalized axiomatic system for processes, and in fact the term process algebra was coined during the research that led to ACP.
Informal description
ACP is fundamentally an algebra, in the sense of universal algebraUniversal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
. This algebra provides a way to describe systems in terms of algebraic process expressions that define compositions of other processes, or of certain primitive elements.
Primitives
ACP uses instantaneous, atomic actions (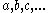 ) as its primitives. Some actions have special meaning, such as the action
) as its primitives. Some actions have special meaning, such as the action 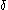 , which represents deadlock
, which represents deadlockDeadlock
A deadlock is a situation where in two or more competing actions are each waiting for the other to finish, and thus neither ever does. It is often seen in a paradox like the "chicken or the egg"...
or stagnation, and the action
 , which represents a silent action (abstracted actions that have no specific identity).
, which represents a silent action (abstracted actions that have no specific identity).Algebraic operators
Actions can be combined to form processes using a variety of operators. These operators can be roughly categorized as providing a basic process algebra, concurrency, and communication.- Choice and sequencing — the most fundamental of algebraic operators are the alternative operator (
 ), which provides a choice between actions, and the sequencing operator (
), which provides a choice between actions, and the sequencing operator ( ), which specifies an ordering on actions. So, for example, the process
), which specifies an ordering on actions. So, for example, the process
- first chooses to perform either
 or
or 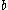 , and then performs action
, and then performs action  . How the choice between
. How the choice between  and
and 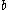 is made does not matter and is left unspecified. Note that alternative composition is commutative but sequential composition is not (because time flows forward).
is made does not matter and is left unspecified. Note that alternative composition is commutative but sequential composition is not (because time flows forward).
- Concurrency — to allow the description of concurrency, ACP provides the merge and left-merge operators. The merge operator,
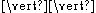 , represents the parallel composition of two processes, the individual actions of which are interleaved. The left-merge operator,
, represents the parallel composition of two processes, the individual actions of which are interleaved. The left-merge operator,  , is an auxiliary operator with similar semantics to the merge, but a commitment to always choose its initial step from the left-hand process. As an example, the process
, is an auxiliary operator with similar semantics to the merge, but a commitment to always choose its initial step from the left-hand process. As an example, the process
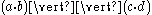
- may perform the actions
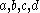 in any of the sequences
in any of the sequences 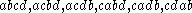 . On the other hand, the process
. On the other hand, the process

- may only perform the sequences
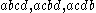 since the left-merge operators ensures that the action
since the left-merge operators ensures that the action  occurs first.
occurs first.
- Communication — interaction (or communication) between processes is represented using the binary communications operator,
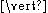 . For example, the actions
. For example, the actions 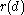 and
and  might be interpreted as the reading and writing of a data item
might be interpreted as the reading and writing of a data item 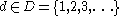 , respectively. Then the process
, respectively. Then the process
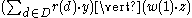
- will communicate the value
 from the right component process to the left component process (i.e. the identifier
from the right component process to the left component process (i.e. the identifier 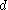 is bound to the value
is bound to the value  , and free instances of
, and free instances of 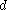 in the process
in the process 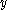 take on that value), and then behave as the merge of
take on that value), and then behave as the merge of 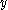 and
and  .
.
- Abstraction — the abstraction operator,
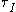 , provides a way to "hide" certain actions, and treat them as events that are internal to the systems being modelled. Abstracted actions are converted to the silent step action
, provides a way to "hide" certain actions, and treat them as events that are internal to the systems being modelled. Abstracted actions are converted to the silent step action  . In some cases, these silent steps can also be removed from the process expression as part of the abstraction process. For example,
. In some cases, these silent steps can also be removed from the process expression as part of the abstraction process. For example,
- which, in this case, can be reduced to
- since the event
 is no longer observable and has no observable effects.
is no longer observable and has no observable effects.
Formal definition
ACP fundamentally adopts an axiomatic, algebraic approach to the formal definition of its various operators. The axioms presented below comprise the full axiomatic system for ACP (ACP with abstraction).
(ACP with abstraction).Basic process algebra
Using the alternative and sequential composition operators, ACP defines a basic process algebra which satisfies the axioms
Deadlock
Beyond the basic algebra, two additional axioms define the relationships between the alternative and sequencing operators, and the deadlock action,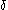
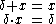
Concurrency and interaction
The axioms associated with the merge, left-merge, and communication operators are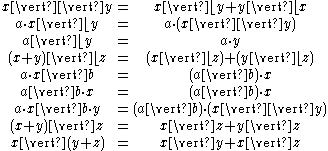
When the communications operator is applied to actions alone, rather than processes, it is interpreted as a binary function from actions to actions,
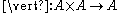 . The definition of this function defines the possible interactions between processes — those pairs of actions that do not constitute interactions are mapped to the deadlock action,
. The definition of this function defines the possible interactions between processes — those pairs of actions that do not constitute interactions are mapped to the deadlock action, 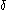 , while permitted interaction pairs are mapped to corresponding single actions representing the occurrence of an interaction. For example, the communications function might specify that
, while permitted interaction pairs are mapped to corresponding single actions representing the occurrence of an interaction. For example, the communications function might specify that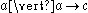
which indicates that a successful interaction
 will be reduced to the action
will be reduced to the action  . ACP also includes an encapsulation operator,
. ACP also includes an encapsulation operator, 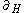 for some
for some 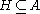 , which is used to convert unsuccessful communication attempts (i.e. elements of
, which is used to convert unsuccessful communication attempts (i.e. elements of  that have not been reduced via the communication function) to the deadlock action. The axioms associated with the communications function and encapsulation operator are
that have not been reduced via the communication function) to the deadlock action. The axioms associated with the communications function and encapsulation operator are
Abstraction
The axioms associated with the abstraction operator are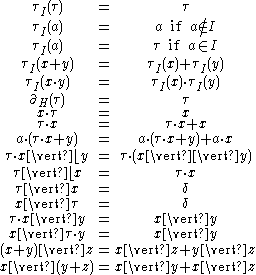
Related formalisms
ACP has served as the basis or inspiration for several other formalisms that can be used to describe and analyze concurrent systems, including:- mCRL2MCRL2mCRL2 is a specification language for describing concurrent discrete event systems. It is accompanied with a toolset, that facilitates tools, techniques and methods for simulation, analysis and visualization of behaviour. The behavioural part of the language is based on process algebra...
- HyPA — a process algebra for hybrid systems