Alternant matrix
Encyclopedia
In linear algebra
, an alternant matrix, is a matrix with a particular structure, in which successive columns have a particular function applied to their entries. An alternant determinant is the determinant
of an alternant matrix. Such a matrix of size m × n matrix may be written out as
or more succinctly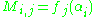
for all indices i and j. (Some authors use the transpose
of the above matrix.)
Examples of alternant matrices include Vandermonde matrices, for which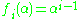
and Moore matrices for which 
.
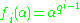If
and the 
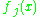functions are all polynomials we have some additional results: if 
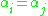for any 
then the determinant of any alternant matrix is zero (as a row is then repeated), thus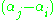 
divides the determinant for all 
. As such, if we take
(a Vandermonde matrix) then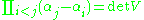
divides such polynomial alternant determinants. The ratio 
is called a bialternant. In the case where each function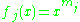 
, this forms the classical definition of the Schur polynomial
s.
Alternant matrices are used in coding theory
in the construction of alternant code
s.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, an alternant matrix, is a matrix with a particular structure, in which successive columns have a particular function applied to their entries. An alternant determinant is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of an alternant matrix. Such a matrix of size m × n matrix may be written out as
or more succinctly
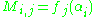
for all indices i and j. (Some authors use the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the above matrix.)
Examples of alternant matrices include Vandermonde matrices, for which
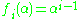and Moore matrices for which 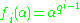.If
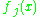and the functions are all polynomials we have some additional results: if 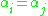for any then the determinant of any alternant matrix is zero (as a row is then repeated), thus 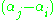divides the determinant for all . As such, if we take(a Vandermonde matrix) then
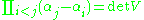divides such polynomial alternant determinants. The ratio is called a bialternant. In the case where each function 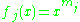, this forms the classical definition of the Schur polynomialSchur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
s.
Alternant matrices are used in coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
in the construction of alternant code
Alternant code
In coding theory, alternant codes form a class of parameterised error-correcting codes which generalise the BCH codes.-Definition:An alternant code over GF of length n is defined by a parity check matrix H of alternant form Hi,j = αjiyi, where the αj are distinct elements of the extension GF, the...
s.