
Alvis–Curtis duality
Encyclopedia
In mathematics, Alvis–Curtis duality is a duality operation
on the characters
of a reductive group
over a finite field
, introduced by and studied by his student . introduced a similar duality operation for Lie algebras.
Alvis–Curtis duality has order 2 and is an isometry on generalized characters.
discusses Alvis–Curtis duality in detail.
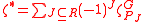
Here the sum is over all subsets J of the set R of simple roots of the Coxeter system of G. The character ζ is the truncation of ζ to the parabolic subgroup PJ of the subset J, given by restricting ζ to PJ and then taking the space of invariants of the unipotent radical of PJ. (The operation of truncation is the adjoint functor of parabolic induction
.)
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
on the characters
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, introduced by and studied by his student . introduced a similar duality operation for Lie algebras.
Alvis–Curtis duality has order 2 and is an isometry on generalized characters.
discusses Alvis–Curtis duality in detail.
Definition
The dual ζ* of a character ζ of a finite group G with a split BN-pair is defined to be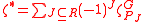
Here the sum is over all subsets J of the set R of simple roots of the Coxeter system of G. The character ζ is the truncation of ζ to the parabolic subgroup PJ of the subset J, given by restricting ζ to PJ and then taking the space of invariants of the unipotent radical of PJ. (The operation of truncation is the adjoint functor of parabolic induction
Parabolic induction
In mathematics, parabolic induction is a method of constructing representations of a reductive group from representations of its parabolic subgroups....
.)
Examples
- The dual of the trivial character 1 is the Steinberg character.
- The dual of a Deligne–Lusztig character R is εGεTR.
- The dual of a cuspidal character χ is (–1)|Δ|χ, where Δ is the set of simple roots.
- The dual of the Gelfand–Graev character is the character taking value |ZF|ql on the regular unipotent elements and vanishing elsewhere.

