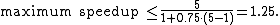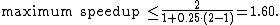Amdahl's law - AbsoluteAstronomy.com

Amdahl's law, also known as Amdahl's argument, is named after computer architect

Computer architecture

In computer science and engineering, computer architecture is the practical art of selecting and interconnecting hardware components to create computers that meet functional, performance and cost goals and the formal modelling of those systems....

Gene Amdahl

Gene Myron Amdahl is a Norwegian-American computer architect and high-tech entrepreneur, chiefly known for his work on mainframe computers at IBM and later his own companies, especially Amdahl Corporation...

, and is used to find the maximum expected improvement to an overall system when only part of the system is improved. It is often used in parallel computing

Parallel computing

Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...

to predict the theoretical maximum speedup using multiple processors.

The speedup of a program using multiple processors in parallel computing is limited by the time needed for the sequential fraction of the program. For example, if a program needs 20 hours using a single processor core, and a particular portion of 1 hour cannot be parallelized, while the remaining promising portion of 19 hours (95%) can be parallelized, then regardless of how many processors we devote to a parallelized execution of this program, the minimum execution time cannot be less than that critical 1 hour. Hence the speedup is limited up to 20×, as the diagram illustrates.

Description

Amdahl's law is a model for the relationship between the expected speedup of parallelized implementations of an algorithm relative to the serial algorithm, under the assumption that the problem size remains the same when parallelized. For example, if for a given problem size a parallelized implementation of an algorithm can run 12% of the algorithm's operations arbitrarily quickly (while the remaining 88% of the operations are not parallelizable), Amdahl's law states that the maximum speedup of the parallelized version is times as fast as the non-parallelized implementation.

More technically, the law is concerned with the speedup achievable from an improvement to a computation that affects a proportion P of that computation where the improvement has a speedup of S. (For example, if an improvement can speed up 30% of the computation, P will be 0.3; if the improvement makes the portion affected twice as fast, S will be 2.) Amdahl's law states that the overall speedup of applying the improvement will be:

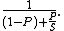
To see how this formula was derived, assume that the running time of the old computation was 1, for some unit of time. The running time of the new computation will be the length of time the unimproved fraction takes (which is 1 − P), plus the length of time the improved fraction takes. The length of time for the improved part of the computation is the length of the improved part's former running time divided by the speedup, making the length of time of the improved part P/S. The final speedup is computed by dividing the old running time by the new running time, which is what the above formula does.

Here's another example. We are given a sequential task which is split into four consecutive parts: P1, P2, P3 and P4 with the percentages of runtime being 11%, 18%, 23% and 48% respectively. Then we are told that P1 is not sped up, so S1 = 1, while P2 is sped up 5×, P3 is sped up 20×, and P4 is sped up 1.6×. By using the formula
P1/S1 + P2/S2 + P3/S3 + P4/S4,
we find the new sequential running time is:

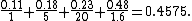
or a little less than ½ the original running time. Using the formula
,
the overall speed boost is
1 / 0.4575 = 2.186,
or a little more than double the original speed.
Notice how the 20× and 5× speedup don't have much effect on the overall speed when P1 (11%) is not sped up, and P4 (48%) is sped up only 1.6 times.

Parallelization

In the case of parallelization, Amdahl's law states that if P is the proportion of a program that can be made parallel (i.e. benefit from parallelization), and (1 − P) is the proportion that cannot be parallelized (remains serial), then the maximum speedup that can be achieved by using N processors is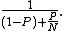

In the limit, as N tends to infinity

Extended real number line

In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...

, the maximum speedup tends to 1 / (1 − P). In practice, performance to price ratio falls rapidly as N is increased once there is even a small component of (1 − P).

As an example, if P is 90%, then (1 − P) is 10%, and the problem can be speed up by a maximum of a factor of 10, no matter how large the value of N used. For this reason, parallel computing is only useful for either small numbers of processor

Central processing unit

The central processing unit is the portion of a computer system that carries out the instructions of a computer program, to perform the basic arithmetical, logical, and input/output operations of the system. The CPU plays a role somewhat analogous to the brain in the computer. The term has been in...

s, or problems with very high values of P: so-called embarrassingly parallel

Embarrassingly parallel

In parallel computing, an embarrassingly parallel workload is one for which little or no effort is required to separate the problem into a number of parallel tasks...

problems. A great part of the craft of parallel programming consists of attempting to reduce the component (1 – P) to the smallest possible value.

P can be estimated by using the measured speedup SU on a specific number of processors NP using

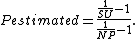
P estimated in this way can then be used in Amdahl's law to predict speedup for a different number of processors.

Relation to law of diminishing returns

Amdahl's law is often conflated with the law of diminishing returns

Diminishing returns

In economics, diminishing returns is the decrease in the marginal output of a production process as the amount of a single factor of production is increased, while the amounts of all other factors of production stay constant.The law of diminishing returns In economics, diminishing returns (also...

, whereas only a special case of applying Amdahl's law demonstrates 'law of diminishing returns'. If one picks optimally (in terms of the achieved speed-up) what to improve, then one will see monotonically decreasing improvements as one improves. If, however, one picks non-optimally, after improving a sub-optimal component and moving on to improve a more optimal component, one can see an increase in return. Note that it is often rational to improve a system in an order that is "non-optimal" in this sense, given that some improvements are more difficult or consuming of development time than others.

Amdahl's law does represent the law of diminishing returns if you are considering what sort of return you get by adding more processors to a machine, if you are running a fixed-size computation that will use all available processors to their capacity. Each new processor you add to the system will add less usable power than the previous one. Each time you double the number of processors the speedup ratio will diminish, as the total throughput heads toward the limit of

.

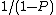This analysis neglects other potential bottlenecks such as memory bandwidth

Memory bandwidth

Memory bandwidth is the rate at which data can be read from or stored into a semiconductor memory by a processor. Memory bandwidth is usually expressed in units of bytes/second, though this can vary for systems with natural data sizes that are not a multiple of the commonly used 8-bit bytes.Memory...

and I/O bandwidth, if they do not scale with the number of processors; however, taking into account such bottlenecks would tend to further demonstrate the diminishing returns of only adding processors.

Speedup in a sequential program

The maximum speedup in an improved sequential program, where some part was sped up

times is limited by inequality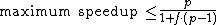

where

(

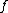) is the fraction of time (before the improvement) spent in the part that was not improved. For example (see picture on right):

If part B is made five times faster (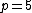), , 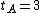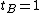and 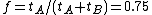, then
If part A is made to run twice as fast (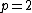), , 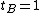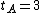and 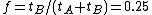, then

Therefore, making A twice as fast is better than making B five times faster. The percentage improvement in speed can be calculated as

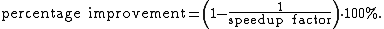
Improving part A by a factor of two will increase overall program speed by a factor of 1.6, which makes it 37.5% faster than the original computation.
However, improving part B by a factor of five, which presumably requires more effort, will only achieve an overall speedup factor of 1.25, which makes it 20% faster.

Criticisms

Danny Hillis (in the 1998 book Pattern on the Stone
The Pattern on the Stone: The Simple Ideas That Make Computers Work
The Pattern on the Stone: The Simple Ideas that Make Computers Work is a book by W. Daniel Hillis, published in 1998 by Basic Books...

) has criticized Amdahl's Law as being unnecessarily pessimistic in its assumption that the sequential portion of a program as being 5% (or 50%) of the execution time. In many applications, particularly with very large data sets (such as Google

Google

Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...

calculating PageRank

PageRank

PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...

, or scientific programs doing FEA), the amount of sequential code is closer to 0%, as essentially every data element can be processed independently.

John L. Gustafson pointed out in 1988 what is now known as Gustafson's Law

Gustafson's law

Gustafson's Law is a law in computer science which says that problems with large, repetitive data sets can be efficiently parallelized. Gustafson's Law contradicts Amdahl's law, which describes a limit on the speed-up that parallelization can provide. Gustafson's law was first described by John...

: people typically are not interested in solving a fixed problem in the shortest possible period of time, as Amdahl's Law describes, but rather in solving the largest possible problem (e.g. the most accurate possible approximation) in a fixed "reasonable" amount of time. If the non-parallelizable portion of the problem is fixed, or grows very slowly with problem size (e.g. O(

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

log n)), then additional processors can increase the possible problem size without limit.

External links

Cases where Amdahl's law is inapplicable
Oral history interview with Gene M. Amdahl Charles Babbage Institute
Charles Babbage Institute
The Charles Babbage Institute is a research center at the University of Minnesota specializing in the history of information technology, particularly the history since 1935 of digital computing, programming/software, and computer networking....

, University of Minnesota. Amdahl discusses his graduate work at the University of Wisconsin and his design of WISC
Wisconsin Integrally Synchronized Computer
The Wisconsin Integrally Synchronized Computer was an early digital computer designed and built at the University of Wisconsin–Madison. Operational in 1954, it was the first digital computer in the state....

. Discusses his role in the design of several computers for IBM including the STRETCH, IBM 701
IBM 701
The IBM 701, known as the Defense Calculator while in development, was announced to the public on April 29, 1952, and was IBM’s first commercial scientific computer...

, and IBM 704
IBM 704
The IBM 704, the first mass-produced computer with floating point arithmetic hardware, was introduced by IBM in 1954. The 704 was significantly improved over the IBM 701 in terms of architecture as well as implementations which were not compatible with its predecessor.Changes from the 701 included...

. He discusses his work with Nathaniel Rochester
Nathaniel Rochester (computer scientist)
Nathan Rochester designed the IBM 701, wrote the first assembler and participated in the founding of the field of artificial intelligence.- Early work :...

and IBM's management of the design process. Mentions work with Ramo-Wooldridge, Aeronutronic
Aeronutronic
Aeronutronic was a defense and space related division of Ford Motor Company set up in 1956. In 1961 Ford purchased Philco and merged the two companies in 1963. Aeronutronic provided major support for the development of Project Space Track...

, and Computer Sciences Corporation
Computer Sciences Corporation
Computer Sciences Corporation is an American information technology and business services company headquartered in Falls Church, Virginia, USA...
Reevaluating Amdahl's Law
Reevaluating Amdahl's Law and Gustafson's Law
A simple interactive Amdahl's Law calculator
"Amdahl's Law" by Joel F. Klein, Wolfram Demonstrations Project
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

, 2007.
Amdahl's Law in the Multicore Era
Amdahl's Law explanation
Blog Post: "What the $#@! is Parallelism, Anyhow?"
Amdahl's Law applied to OS system calls on multicore CPU