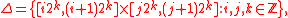Analyst's traveling salesman theorem
Encyclopedia
The Analyst's Traveling Salesman Problem is an analog of the traveling salesman problem in combinatorial optimization
. In its simplest and original form, it asks under what conditions may a set E in two-dimensional Euclidean space
 be contained inside a rectifiable curve
be contained inside a rectifiable curve
of finite length. So while in the original traveling salesman problem, one asks for the shortest way to visit every vertex in a graph with a discrete path, this analytical version requires the curve to visit perhaps infinitely many points.
s at H1-almost every point in Γ (where H1 denotes one-dimensional hausdorff measure
), E must look flat when you zoom in on points in E. This suggests that a condition that would tell us whether a set could be contained in a curve must somehow incorporate information about how flat E is when we zoom in on points of E at different scales.
This discussion motivates the definition of the following quantity:
Where Q is any square, is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively,
is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively, 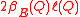 is the width of the smallest rectangle containing the portion of E inside Q, and hence
is the width of the smallest rectangle containing the portion of E inside Q, and hence 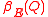 gives us a scale invariant notion of flatness.
gives us a scale invariant notion of flatness.
where denotes the set of integers. For a set
denotes the set of integers. For a set 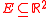 , define
, define

where diam E is the diameter
of E. Then Peter Jones' Analyst's Traveling Salesman Theorem may be stated as follows:
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
. In its simplest and original form, it asks under what conditions may a set E in two-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
 be contained inside a rectifiable curve
be contained inside a rectifiable curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
of finite length. So while in the original traveling salesman problem, one asks for the shortest way to visit every vertex in a graph with a discrete path, this analytical version requires the curve to visit perhaps infinitely many points.
β-numbers
A posteriori, for E to be contained in a rectifiable curve Γ, since Γ has tangentTangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
s at H1-almost every point in Γ (where H1 denotes one-dimensional hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
), E must look flat when you zoom in on points in E. This suggests that a condition that would tell us whether a set could be contained in a curve must somehow incorporate information about how flat E is when we zoom in on points of E at different scales.
This discussion motivates the definition of the following quantity:

Where Q is any square,
 is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively,
is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively, 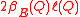 is the width of the smallest rectangle containing the portion of E inside Q, and hence
is the width of the smallest rectangle containing the portion of E inside Q, and hence 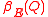 gives us a scale invariant notion of flatness.
gives us a scale invariant notion of flatness.Jones' traveling salesman theorem in R2
Let Δ denote the collection of dyadic squares, that is,where
 denotes the set of integers. For a set
denotes the set of integers. For a set 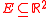 , define
, define
where diam E is the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of E. Then Peter Jones' Analyst's Traveling Salesman Theorem may be stated as follows:
- There is a number C > 0 such that whenever E is a set with such that β(E) < ∞, E can be contained in a curve with length no more than Cβ(E).
- Conversely (and substantially more difficult to prove), if Γ is a rectifiable curve, then β(Γ) < CH1(Γ).
Euclidean space and Hilbert space
- The Traveling Salesman Theorem was shown to hold in general Euclidean spaces by Kate Okikiolu, that is, the same theorem above holds for sets
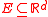 , d > 1, where Δ is now the collection of dyadic cubes in
, d > 1, where Δ is now the collection of dyadic cubes in 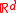 defined in a similar way as dyadic squares. In her proof, the constant C grows exponentially with the dimension d.
defined in a similar way as dyadic squares. In her proof, the constant C grows exponentially with the dimension d.
- With some slight modifications to the definition of β(E), Raanan Schul showed Traveling Salesman Theorem also holds for sets E that lie in any Hilbert SpaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and in particular, implies the theorems of Jones and Okikiolu, where now the constant C is independent of dimension. (In particular, this involves using β-numbers of balls instead of cubes).
Menger curvature and metric spaces
- Hahlomaa further adjusted the definition of β(E) to get a condition for when a set E of an arbitrary metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
may be contained in the LipschitzLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
-image of a subset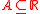 of positive measure. For this, he had to redefine the definition of the β-numbers using menger curvatureMenger curvatureIn mathematics, the Menger curvature of a triple of points in n-dimensional Euclidean space Rn is the reciprocal of the radius of the circle that passes through the three points...
of positive measure. For this, he had to redefine the definition of the β-numbers using menger curvatureMenger curvatureIn mathematics, the Menger curvature of a triple of points in n-dimensional Euclidean space Rn is the reciprocal of the radius of the circle that passes through the three points...
(since in a metric space there isn't necessarily a notion of a cube or a straight line).
- Menger curvatureMenger curvatureIn mathematics, the Menger curvature of a triple of points in n-dimensional Euclidean space Rn is the reciprocal of the radius of the circle that passes through the three points...
, as in the previous example, can be used to give numerical estimates that determine whether a set contains a rectifiable subset, and the proofs of these results frequently depend on β-numbers.