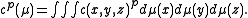Menger curvature
Encyclopedia
In mathematics
, the Menger curvature of a triple of points in n-dimension
al Euclidean space
Rn is the reciprocal
of the radius
of the circle that passes through the three points. It is named after the Austria
n-American
mathematician
Karl Menger
.
spanned by x, y and z and let C ⊆ Π be the unique Euclidean circle
in Π that passes through x, y and z (the circumcircle
of x, y and z). Let R be the radius of C. Then the Menger curvature c(x, y, z) of x, y and z is defined by
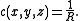
If the three points are collinear
, R can be informally considered to be +∞, and it makes rigorous sense to define c(x, y, z) = 0. If any of the points x, y and z are coincident, again define c(x, y, z) = 0.
Using the well-known formula relating the side lengths of a triangle
to its area, it follows that
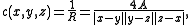
where A denotes the area of the triangle spanned by x, y and z.
Another way of computing Menger curvature is the identity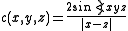
where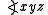
is the angle made at the y-corner of the triangle spanned by x,y,z.
Menger curvature may also be defined on a general metric space
. If X is a metric space and x,y, and z are distinct points, let f be an isometry
from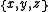
into 
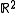. Define the Menger curvature of these points to be
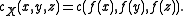
Note that f need not be defined on all of X, just on {x,y,z}, and the value cX (x,y,z) is independent of the choice of f.
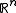may be rectifiable
. For a Borel measure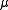
on a Euclidean space 
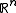define
The basic intuition behind the result is that Menger curvature measures how straight a given triple of points are (the smaller
is, the closer x,y, and z are to being collinear), and this integral quantity being finite is saying that the set E is flat on most small scales. In particular, if the power in the integral is larger, our set is smoother than just being rectifiable
In the opposite direction, there is a result of Peter Jones:
Analogous results hold in general metric spaces:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Menger curvature of a triple of points in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circle that passes through the three points. It is named after the Austria
Austria
Austria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
n-American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Karl Menger
Karl Menger
Karl Menger was a mathematician. He was the son of the famous economist Carl Menger. He is credited with Menger's theorem. He worked on mathematics of algebras, algebra of geometries, curve and dimension theory, etc...
.
Definition
Let x, y and z be three points in Rn; for simplicity, assume for the moment that all three points are distinct and do not lie on a single straight line. Let Π ⊆ Rn be the Euclidean planePlane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
spanned by x, y and z and let C ⊆ Π be the unique Euclidean circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
in Π that passes through x, y and z (the circumcircle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
of x, y and z). Let R be the radius of C. Then the Menger curvature c(x, y, z) of x, y and z is defined by
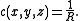
If the three points are collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, R can be informally considered to be +∞, and it makes rigorous sense to define c(x, y, z) = 0. If any of the points x, y and z are coincident, again define c(x, y, z) = 0.
Using the well-known formula relating the side lengths of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
to its area, it follows that
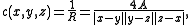
where A denotes the area of the triangle spanned by x, y and z.
Another way of computing Menger curvature is the identity
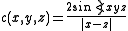
where
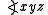is the angle made at the y-corner of the triangle spanned by x,y,z.Menger curvature may also be defined on a general metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. If X is a metric space and x,y, and z are distinct points, let f be an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
from
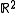into . Define the Menger curvature of these points to be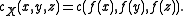Note that f need not be defined on all of X, just on {x,y,z}, and the value cX (x,y,z) is independent of the choice of f.
Integral Curvature Rectifiability
Menger curvature can be used to give quantitative conditions for when sets in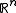 may be rectifiableRectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
. For a Borel measure
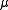on a Euclidean space 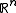define
- A Borel set
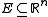is rectifiable if 
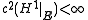, where 
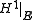denotes one-dimensional Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
restricted to the set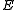
..
The basic intuition behind the result is that Menger curvature measures how straight a given triple of points are (the smaller
is, the closer x,y, and z are to being collinear), and this integral quantity being finite is saying that the set E is flat on most small scales. In particular, if the power in the integral is larger, our set is smoother than just being rectifiable- Let
, 
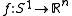be a homeomorphism and 
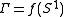. Then 
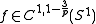if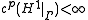 
.
- If
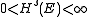where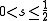 
, and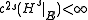 
, then 
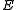is rectifiable in the sense that there are countably many 
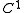curves 
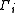such that 
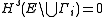. The result is not true for 
, and 
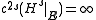for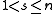 
.:
In the opposite direction, there is a result of Peter Jones:
- If
, 
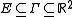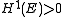, and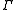 
is rectifiable. Then there is a positive Radon measure 
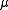supported on 
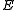satisfying 
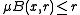for all 
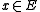and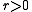 
such that 
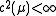(in particular, this measure is the Frostman measure associated to E). Moreover, if 
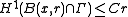for some constant C and all 
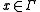and r>0, then 
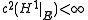. This last result follows from the Analyst's Traveling Salesman Theorem.
Analogous results hold in general metric spaces: