André Joyal
Encyclopedia
André Joyal is a professor of mathematics
at the Université du Québec à Montréal
who works on category theory. Joyal was born in Drummondville (formerly Saint-Majorique). He has three children and lives in Montreal.
and with M. Tierney a generalization of the Galois theory of Grothendieck
in the setup of locales. Most of his research is in some way related to category theory, higher category theory and their applications. He did the first real work on quasi-categories, after their invention by Boardman and Vogt, in particular conjecturing. and proving the existence of a Quillen model structure on sSet whose weak equivalences generalize both equivalence of categories and Kan equivalence of spaces. He co-authored the book "Algebraic Set Theory" with Ieke Moerdijk
and recently started a web-based expositional project Joyal's CatLab on categorical mathematics.
If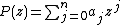
is a polynomial of degree n such that 
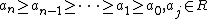, then all the zeros of P(z) lie in 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
at the Université du Québec à Montréal
Université du Québec à Montréal
The Université du Québec à Montréal is one of four universities in Montreal, Quebec, Canada.-Basic facts:The UQAM is the largest constituent element of the Université du Québec , a public university system with other branches in Gatineau , Rimouski, Rouyn-Noranda, Quebec City, Chicoutimi, and...
who works on category theory. Joyal was born in Drummondville (formerly Saint-Majorique). He has three children and lives in Montreal.
Main research
He invented Kripke–Joyal semantics, the theory of combinatorial speciesCombinatorial species
In combinatorial mathematics, the theory of combinatorial species is an abstract, systematic method for analysing discrete structures in terms of generating functions. Examples of discrete structures are graphs, permutations, trees, and so on; each of these has an associated generating function...
and with M. Tierney a generalization of the Galois theory of Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
in the setup of locales. Most of his research is in some way related to category theory, higher category theory and their applications. He did the first real work on quasi-categories, after their invention by Boardman and Vogt, in particular conjecturing. and proving the existence of a Quillen model structure on sSet whose weak equivalences generalize both equivalence of categories and Kan equivalence of spaces. He co-authored the book "Algebraic Set Theory" with Ieke Moerdijk
Ieke Moerdijk
Izak Moerdijk is professor of Mathematics at the Mathematisch Instituut of the Radboud University Nijmegen. He is the author of several influential books.-Selected works:...
and recently started a web-based expositional project Joyal's CatLab on categorical mathematics.
Works on algebraic equations
Joyal proved the following theorem in 1967.If
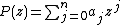is a polynomial of degree n such that 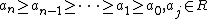, then all the zeros of P(z) lie in .External links
- Picture of André Joyal
- Interview with André Joyal (in French)
- Page on André Joyal at nLabNLabnLab is a wiki-lab of a novel kind, for collaborative work on mathematics, physics, and philosophy, including original research, with a focus on category theory. The nLab espouses the n-point of view : that category theory and higher category theory provide a useful unifying viewpoint for...