Combinatorial species
Encyclopedia
In combinatorial
mathematics
, the theory of combinatorial species is an abstract, systematic method for analysing discrete structures in terms of generating function
s. Examples of discrete structures are (finite) graphs
, permutation
s, trees
, and so on; each of these has an associated generating function which counts how many structures there are of a certain size. One goal of species theory is to be able to analyse complicated structures by describing them in terms of transformations and combinations of simpler structures. These operations correspond to equivalent manipulations of generating functions, so producing such functions for complicated structures is much easier than with other methods. The theory was introduced by André Joyal
.
The power of the theory comes from its level of abstraction. The "description format" of a structure (such as adjacency list
versus adjacency matrix
for graphs) is irrelevant, because species are purely algebraic. Category theory
provides a useful language for the concepts that arise here, but it is not necessary to understand categories before being able to work with species.
This leads to the formal definition of a combinatorial species. Let
be the category of finite sets and bijection
s (the collection of all finite sets, and invertible functions between them). A species is a functor
given a set A, it yields the set F[A] of F-structures on A. A functor also operates on bijections. If φ is a bijection between sets A and B, then F[φ] is a bijection between the sets of F-structures F[A] and F[B], called transport of F-structures along φ.
For example, the "species of permutations" maps each finite set A to the set of all permutations of A, and each bijection from A to another set B naturally induces a bijection from the set of all permutations of A to the set of all permutations of B. Similarly, the "species of partitions" can be defined by assigning to each finite set the set of all its partition
s, and the "power set species" assigns to each finite set its power set.
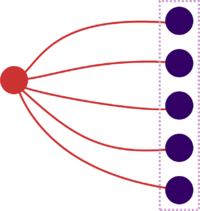
There is a standard way of illustrating an instance of any structure, regardless of its nature. The diagram below shows a structure on a set of five elements: arcs connect the structure (red) to the elements (blue) from which it is built.
The choice of 
as the category on which species operate is important. Because a bijection can only exist between two sets when they have the same size, the number of elements in F[A] depends only on the size of A. (This follows from the formal definition of a functor.) Restriction to finite sets means that |F[A]| is always finite, so it is possible to do arithmetic with such quantities. In particular, the exponential generating series F(x) of a species F can be defined:
where
is the size of F[A] for any set A having n elements.
Some examples:
of sets, and corresponds to a choice between structures. For species F and G, define (F + G)[A] to be the disjoint union (also written "+") of F[A] and G[A]. It follows that (F + G)(x) = F(x) + G(x). As a demonstration, take E+ to be the species of non-empty sets, whose generating function is E+(x) = ex − 1, and 1 the species of the empty set
, whose generating function is 1(x) = 1. It follows that E = 1 + E+: in words, "a set is either empty or non-empty". Equations like this can be read as referring to a single structure, as well as to the entire collection of structures.
Multiplying species is slightly more complicated. It is possible to just take the Cartesian product of sets as the definition, but the combinatorial interpretation of this is not quite right. (See below for the use of this kind of product.) Rather than putting together two unrelated structures on the same set, the multiplication operator uses the idea of splitting the set into two components, constructing an F-structure on one and a G-structure on the other.
This is a disjoint union over all possible binary partitions of A. It is straightforward to show that multiplication is associative
and commutative
(up to
isomorphism
), and distributive
over addition. As for the generating series, (F · G)(x) = F(x)G(x).
The diagram below shows one possible (F · G)-structure on a set with five elements. The F-structure (red) picks up three elements of the base set, and the G-structure (light blue) takes the rest. Other structures will have F and G splitting the set in a different way. The set (F · G)[A], where A is the base set, is the disjoint union of all such structures.
Composition, also called substitution, is more complicated again. The basic idea is to replace components of F with G-structures, forming (F∘G). As with multiplication, this is done by splitting the input set A; the disjoint subsets are given to G to make G-structures, and the set of subsets is given to F, to make the F-structure linking the G-structures. It is required for G to map the empty set to itself, in order for composition to work. The formal definition is:
Here, P is the species of partitions, so P[A] is the set of all partitions of A. This definition says that an element of (F∘G)[A] is made up of an F-structure on some partition of A, and a G-structure on each component of the partition. The generating series is
.
One such structure is shown below. Three G-structures (light blue) divide up the five-element base set between them; then, an F-structure (red) is built to connect the G-structures.
These last two operations may be illustrated by the example of trees. First, define X to be the species "singleton" whose generating series is X(x) = x. Then the species Ar of rooted trees (from the French "arborescence") is defined recursively by Ar = X · E(Ar). This equation says that a tree consists of a single root and a set of (sub-)trees. The recursion does not need an explicit base case: it only generates trees in the context of being applied to some finite set. One way to think about this is that the Ar functor is being applied repeatedly to a "supply" of elements from the set — each time, one element is taken by X, and the others distributed by E among the Ar subtrees, until there are no more elements to give to E. This shows that algebraic descriptions of species are quite different from type specifications in programming languages like Haskell
.
Likewise, the species P can be characterised as P = E(E+): "a partition is a pairwise disjoint set of nonempty sets (using up all the elements of the input set)". The exponential generating series for P is
, which is the series for the Bell numbers.
Differentiation
is an operation that makes more sense for series than it does for species. To differentiate an exponential series, the sequence of coefficients needs to be shifted one place to the "left" (losing the first term). This suggests a definition for species: F' [A] = F[A + {*}], where {*} is a singleton set and "+" is disjoint union. The more advanced parts of the theory of species use differentiation extensively, to construct and solve differential equation
s on species and series. The idea of adding (or removing) a single part of a structure is a powerful one: it can be used to establish relationships between seemingly unconnected species.
For example, consider a structure of the species L of linear orders—lists of elements of the ground set. Removing an element of a list splits it into two parts (possibly empty); in symbols, this is L = L·L. The exponential generating function of L is L(x) = 1/(1 − x), and indeed:
The species C of cyclic permutations takes a set A to the set of all cycles on A. Removing a single element from a cycle reduces it to a list: C = L. We can integrate
the generating function of L to produce that for C.
s.
Pointing selects a single element in a structure. Given a species F, the corresponding pointed species F• is defined by F•[A] = A × F[A]. Thus each F•-structure is an F-structure with one element distinguished. Pointing is related to differentiation by the relation F• = X·F' , so F•(x) = x F' (x). The species of pointed set
s, E•, is particularly important as a building block for many of the more complex constructions.
The Cartesian product of two species is a species which can build two structures on the same set at the same time. It is different from the ordinary multiplication operator in that all elements of the base set are shared between the two structures. An (F × G)-structure can be seen as a superposition of an F-structure and a G-structure. Bigraphs could be described as the superposition of a graph and a set of trees: each node of the bigraph is part of a graph, and at the same time part of some tree that describes how nodes are nested. The generating function (F × G)(x) is the Hadamard or coefficient-wise product of F(x) and G(x).
The species E• × E• can be seen as making two independent selections from the base set. The two points might coincide, unlike in X·X·E, where they are forced to be different.
As functors, species F and G may be combined by functorial composition:
(the box symbol is used, because the circle is already in use for substitution). This constructs an F-structure on the set of all G-structures on the set A. For example, if F is the functor taking a set to its power set, a structure of the composed species is some subset of the G-structures on A. If we now take G to be E• × E• from above, we obtain the species of directed graphs, with self-loops permitted. (A directed graph is a set of edges, and edges are pairs of nodes: so a graph is a subset of the set of pairs of elements of the node set A.) Other families of graphs, as well as many other structures, can be defined in this way.
There is an exact correspondence between trees in the first class and permutations of A. Any of these trees can be constructed from any of the others, by permuting the labels on its nodes. For any two trees s and t in this class, there is some permutation σ in the symmetric group
SA which acts on
s to give t: Ar[σ](s) = t. The same holds for the second class of trees. This property can be used to define an equivalence relation
on Ar[A], dividing it into the two parts listed above. These equivalence classes are the isomorphism types of Ar-structures of order 3.
Formally, when F is a species, we define T(Fn) to be the quotient set F[{1, ..., n}]/~ of types of F-structures of order n, where "~" is the relation "s ~ t if and only if
there is some σ in Sn such that F[σ](s) = t". As with the exponential generating functions, the size of T(Fn) depends only on the value of n and the definition of F. It is the set of unlabelled F-structures on any set of size n.
The isomorphism type generating series of F is:
Manipulations of these functions are done in essentially the same way as for the exponential generating functions. There are a few differences in how some of the operations translate into operations on type generating series. Addition and multiplication work as expected, but the more complicated operations need some more sophisticated mathematical tools for their proper definitions.
There is a much more general series, called the cycle index series, for each species, which contains all the information in the previously-defined series, and more. Any permutation σ of a finite set A with n elements can be decomposed, uniquely, into a product of disjoint cycles. Letting σi be the number of cycles of length i in the decomposition of σ ∈ Sn, the cycle type of σ is defined to be the sequence (σ1, σ2, ..., σn). Now let Fix(σ) be the set of elements fixed by σ — that is, the elements x of A where σ(x) = x. Then the cycle index series of F is:
Note that |Fix(F[σ])| is the number of F-structures on A = {1, ..., n} for which σ is an automorphism
.
It follows immediately that
and
for any species F. The cycle index series follows these rules for combinatorial operations on species F and G:
Then the rules for type generating series can be given in terms of these:
whose objects are species and whose arrows are natural transformation
s. This idea can be extended to a bicategory
of certain categories, functors, and natural transformations, to be able to include species over categories other than
. The unary and binary operations defined above can be specified in categorical terms as universal constructions
, much like the corresponding operations for other algebraic systems.
Though the categorical approach brings powerful proof techniques, its level of abstraction means that concrete combinatorial results can be difficult to produce. Instead, the class of species can be described as a semiring
— an algebraic object with two monoid
al operations — in order to focus on combinatorial constructions. The two monoids are addition and multiplication of species. It is easy to show that these are associative, yielding a double semigroup
structure; and then the identities are the species 0 and 1 respectively. Here, 0 is the empty species, taking every set to the empty set (so that no structures can be built on any set), and 1 is the empty set species, which is equal to 0 except that it takes
to 
(it constructs the empty set whenever possible). The two monoids interact in the way required of a semiring: addition is commutative, multiplication distributes over addition, and 0 multiplied by anything yields 0.
The natural number
s can be seen as a subsemiring of the semiring of species, if we identify the natural number n with the n-fold sum 1 + ... + 1 = n 1. This embedding of natural number arithmetic into species theory suggests that other kinds of arithmetic, logic, and computation might also be present. There is also a clear connection between the category-theoretic formulation of species as a functor category, and results relating certain such categories to topoi
and Cartesian closed categories
— connecting species theory with the lambda calculus
and related systems.
Given that natural number species can be added, we immediately have a limited form of subtraction: just as the natural number system admits subtraction for certain pairs of numbers, subtraction can be defined for the corresponding species. If n and m are natural numbers with n larger than m, we can say that n 1 − m 1 is the species (n − m) 1. (If the two numbers are the same, the result is 0 — the identity for addition.) In the world of species, this makes sense because m 1 is a subspecies of n 1; likewise, knowing that E = 1 + E+, we could say that E+ = E − 1.
Going further, subtraction can be defined for all species so that the correct algebraic laws apply. Virtual species are an extension to the species concept that allow inverses to exist for addition, as well as having many other useful properties. If S is the semiring of species, then the ring V of virtual species is (S × S) / ~, where "~" is the equivalence relation
~ (H, K) if and only if F + K is isomorphic to G + H.
The equivalence class of (F, G) is written "F − G". A species F of S appears as F − 0 in V, and its additive inverse is 0 − F.
Addition of virtual species is by component:
+ (H − K) = (F + H) − (G + K).
In particular, the sum of F − 0 and 0 − F is the virtual species F − F, which is the same as 0 − 0: this is the zero of V. Multiplication is defined as·(H − K) = (F·H + G·K) − (F·K + G·H)
and its unit is 1 − 0. Together, these make V into a commutative ring, which as an algebraic structure is much easier to deal with than a semiring. Other operations carry over from species to virtual species in a very natural way, as do the associated power series. "Completing" the class of species like this also means that certain differential equations insoluble over S do have solutions in V.
to 
: other categories can replace these, to obtain species of a different nature.
.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the theory of combinatorial species is an abstract, systematic method for analysing discrete structures in terms of generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s. Examples of discrete structures are (finite) graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s, trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, and so on; each of these has an associated generating function which counts how many structures there are of a certain size. One goal of species theory is to be able to analyse complicated structures by describing them in terms of transformations and combinations of simpler structures. These operations correspond to equivalent manipulations of generating functions, so producing such functions for complicated structures is much easier than with other methods. The theory was introduced by André Joyal
André Joyal
André Joyal is a professor of mathematics at the Université du Québec à Montréal who works on category theory. Joyal was born in Drummondville . He has three children and lives in Montreal.- Main research :...
.
The power of the theory comes from its level of abstraction. The "description format" of a structure (such as adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
versus adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
for graphs) is irrelevant, because species are purely algebraic. Category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
provides a useful language for the concepts that arise here, but it is not necessary to understand categories before being able to work with species.
Definition of species
Any structure — an instance of a particular species — is associated with some set, and there are often many possible structures for the same set. For example, it is possible to construct several different graphs whose node labels are drawn from the same given set. At the same time, any set could be used to build the structures. The difference between one species and another is that they build a different set of structures out of the same base set.This leads to the formal definition of a combinatorial species. Let
be the category of finite sets and bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s (the collection of all finite sets, and invertible functions between them). A species is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
given a set A, it yields the set F[A] of F-structures on A. A functor also operates on bijections. If φ is a bijection between sets A and B, then F[φ] is a bijection between the sets of F-structures F[A] and F[B], called transport of F-structures along φ.
For example, the "species of permutations" maps each finite set A to the set of all permutations of A, and each bijection from A to another set B naturally induces a bijection from the set of all permutations of A to the set of all permutations of B. Similarly, the "species of partitions" can be defined by assigning to each finite set the set of all its partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
s, and the "power set species" assigns to each finite set its power set.
There is a standard way of illustrating an instance of any structure, regardless of its nature. The diagram below shows a structure on a set of five elements: arcs connect the structure (red) to the elements (blue) from which it is built.
as the category on which species operate is important. Because a bijection can only exist between two sets when they have the same size, the number of elements in F[A] depends only on the size of A. (This follows from the formal definition of a functor.) Restriction to finite sets means that |F[A]| is always finite, so it is possible to do arithmetic with such quantities. In particular, the exponential generating series F(x) of a species F can be defined:where
is the size of F[A] for any set A having n elements.Some examples:
- The species of sets (traditionally called E, from the French "ensemble", meaning "set") is the functor which maps A to {A}. Then
, so 
. - The species S of permutations, described above, has
. 
. - The species T2 of pairs (2-tupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s) is the functor taking a set A to A2. Then
and 
.
Calculus of species
Arithmetic on generating functions corresponds to certain "natural" operations on species. The basic operations are addition, multiplication, composition, and differentiation; it is also necessary to define equality on species. Category theory already has a way of describing when two functors are equivalent: a natural isomorphism. In this context, it just means that for each A there is a bijection between F-structures on A and G-structures on A, which is "well-behaved" in its interaction with transport. Note that species with the same generating function might not be isomorphic, but isomorphic species do always have the same generating function.Basic operations
Addition of species is defined by the disjoint unionDisjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of sets, and corresponds to a choice between structures. For species F and G, define (F + G)[A] to be the disjoint union (also written "+") of F[A] and G[A]. It follows that (F + G)(x) = F(x) + G(x). As a demonstration, take E+ to be the species of non-empty sets, whose generating function is E+(x) = ex − 1, and 1 the species of the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, whose generating function is 1(x) = 1. It follows that E = 1 + E+: in words, "a set is either empty or non-empty". Equations like this can be read as referring to a single structure, as well as to the entire collection of structures.
Multiplying species is slightly more complicated. It is possible to just take the Cartesian product of sets as the definition, but the combinatorial interpretation of this is not quite right. (See below for the use of this kind of product.) Rather than putting together two unrelated structures on the same set, the multiplication operator uses the idea of splitting the set into two components, constructing an F-structure on one and a G-structure on the other.
This is a disjoint union over all possible binary partitions of A. It is straightforward to show that multiplication is associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
(up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
), and distributive
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition. As for the generating series, (F · G)(x) = F(x)G(x).
The diagram below shows one possible (F · G)-structure on a set with five elements. The F-structure (red) picks up three elements of the base set, and the G-structure (light blue) takes the rest. Other structures will have F and G splitting the set in a different way. The set (F · G)[A], where A is the base set, is the disjoint union of all such structures.
Composition, also called substitution, is more complicated again. The basic idea is to replace components of F with G-structures, forming (F∘G). As with multiplication, this is done by splitting the input set A; the disjoint subsets are given to G to make G-structures, and the set of subsets is given to F, to make the F-structure linking the G-structures. It is required for G to map the empty set to itself, in order for composition to work. The formal definition is:
Here, P is the species of partitions, so P[A] is the set of all partitions of A. This definition says that an element of (F∘G)[A] is made up of an F-structure on some partition of A, and a G-structure on each component of the partition. The generating series is
.One such structure is shown below. Three G-structures (light blue) divide up the five-element base set between them; then, an F-structure (red) is built to connect the G-structures.
These last two operations may be illustrated by the example of trees. First, define X to be the species "singleton" whose generating series is X(x) = x. Then the species Ar of rooted trees (from the French "arborescence") is defined recursively by Ar = X · E(Ar). This equation says that a tree consists of a single root and a set of (sub-)trees. The recursion does not need an explicit base case: it only generates trees in the context of being applied to some finite set. One way to think about this is that the Ar functor is being applied repeatedly to a "supply" of elements from the set — each time, one element is taken by X, and the others distributed by E among the Ar subtrees, until there are no more elements to give to E. This shows that algebraic descriptions of species are quite different from type specifications in programming languages like Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
.
Likewise, the species P can be characterised as P = E(E+): "a partition is a pairwise disjoint set of nonempty sets (using up all the elements of the input set)". The exponential generating series for P is
, which is the series for the Bell numbers.Differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is an operation that makes more sense for series than it does for species. To differentiate an exponential series, the sequence of coefficients needs to be shifted one place to the "left" (losing the first term). This suggests a definition for species: F' [A] = F[A + {*}], where {*} is a singleton set and "+" is disjoint union. The more advanced parts of the theory of species use differentiation extensively, to construct and solve differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s on species and series. The idea of adding (or removing) a single part of a structure is a powerful one: it can be used to establish relationships between seemingly unconnected species.
For example, consider a structure of the species L of linear orders—lists of elements of the ground set. Removing an element of a list splits it into two parts (possibly empty); in symbols, this is L = L·L. The exponential generating function of L is L(x) = 1/(1 − x), and indeed:
The species C of cyclic permutations takes a set A to the set of all cycles on A. Removing a single element from a cycle reduces it to a list: C = L. We can integrate
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
the generating function of L to produce that for C.
Further operations
There are a variety of other manipulations which may be performed on species. These are necessary to express more complicated structures, such as directed graphs or bigraphBigraph
A bigraph can be modelled as the superposition of a graph and a set of trees ....
s.
Pointing selects a single element in a structure. Given a species F, the corresponding pointed species F• is defined by F•[A] = A × F[A]. Thus each F•-structure is an F-structure with one element distinguished. Pointing is related to differentiation by the relation F• = X·F' , so F•(x) = x F' (x). The species of pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s, E•, is particularly important as a building block for many of the more complex constructions.
The Cartesian product of two species is a species which can build two structures on the same set at the same time. It is different from the ordinary multiplication operator in that all elements of the base set are shared between the two structures. An (F × G)-structure can be seen as a superposition of an F-structure and a G-structure. Bigraphs could be described as the superposition of a graph and a set of trees: each node of the bigraph is part of a graph, and at the same time part of some tree that describes how nodes are nested. The generating function (F × G)(x) is the Hadamard or coefficient-wise product of F(x) and G(x).
The species E• × E• can be seen as making two independent selections from the base set. The two points might coincide, unlike in X·X·E, where they are forced to be different.
As functors, species F and G may be combined by functorial composition:
(the box symbol is used, because the circle is already in use for substitution). This constructs an F-structure on the set of all G-structures on the set A. For example, if F is the functor taking a set to its power set, a structure of the composed species is some subset of the G-structures on A. If we now take G to be E• × E• from above, we obtain the species of directed graphs, with self-loops permitted. (A directed graph is a set of edges, and edges are pairs of nodes: so a graph is a subset of the set of pairs of elements of the node set A.) Other families of graphs, as well as many other structures, can be defined in this way.Types and unlabelled structures
Instead of counting all the possible structures that can be built on some set, we often want to count only the number of different "shapes" of structure. Consider the set of rooted trees on the set A = {a, b, c}. There are nine of these, which can be grouped into two classes by tree shape. There are:- Six trees with three levels:
- a → b → c
- a → c → b
- b → a → c
- b → c → a
- c → a → b
- c → b → a
- Three trees with two levels: (not six, because subtrees are not in any order)
- b ← a → c
- a ← b → c
- a ← c → b
There is an exact correspondence between trees in the first class and permutations of A. Any of these trees can be constructed from any of the others, by permuting the labels on its nodes. For any two trees s and t in this class, there is some permutation σ in the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
SA which acts on
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s to give t: Ar[σ](s) = t. The same holds for the second class of trees. This property can be used to define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on Ar[A], dividing it into the two parts listed above. These equivalence classes are the isomorphism types of Ar-structures of order 3.
Formally, when F is a species, we define T(Fn) to be the quotient set F[{1, ..., n}]/~ of types of F-structures of order n, where "~" is the relation "s ~ t if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is some σ in Sn such that F[σ](s) = t". As with the exponential generating functions, the size of T(Fn) depends only on the value of n and the definition of F. It is the set of unlabelled F-structures on any set of size n.
The isomorphism type generating series of F is:
Manipulations of these functions are done in essentially the same way as for the exponential generating functions. There are a few differences in how some of the operations translate into operations on type generating series. Addition and multiplication work as expected, but the more complicated operations need some more sophisticated mathematical tools for their proper definitions.
There is a much more general series, called the cycle index series, for each species, which contains all the information in the previously-defined series, and more. Any permutation σ of a finite set A with n elements can be decomposed, uniquely, into a product of disjoint cycles. Letting σi be the number of cycles of length i in the decomposition of σ ∈ Sn, the cycle type of σ is defined to be the sequence (σ1, σ2, ..., σn). Now let Fix(σ) be the set of elements fixed by σ — that is, the elements x of A where σ(x) = x. Then the cycle index series of F is:
Note that |Fix(F[σ])| is the number of F-structures on A = {1, ..., n} for which σ is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
.
It follows immediately that
and
for any species F. The cycle index series follows these rules for combinatorial operations on species F and G:
Then the rules for type generating series can be given in terms of these:
Class of all species
There are many ways of thinking about the class of all combinatorial species. Since a species is a functor, it makes sense to say that the category of species is a functor categoryFunctor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
whose objects are species and whose arrows are natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s. This idea can be extended to a bicategory
Bicategory
In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
of certain categories, functors, and natural transformations, to be able to include species over categories other than
. The unary and binary operations defined above can be specified in categorical terms as universal constructionsUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, much like the corresponding operations for other algebraic systems.
Though the categorical approach brings powerful proof techniques, its level of abstraction means that concrete combinatorial results can be difficult to produce. Instead, the class of species can be described as a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
— an algebraic object with two monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
al operations — in order to focus on combinatorial constructions. The two monoids are addition and multiplication of species. It is easy to show that these are associative, yielding a double semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
structure; and then the identities are the species 0 and 1 respectively. Here, 0 is the empty species, taking every set to the empty set (so that no structures can be built on any set), and 1 is the empty set species, which is equal to 0 except that it takes
to (it constructs the empty set whenever possible). The two monoids interact in the way required of a semiring: addition is commutative, multiplication distributes over addition, and 0 multiplied by anything yields 0.The natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s can be seen as a subsemiring of the semiring of species, if we identify the natural number n with the n-fold sum 1 + ... + 1 = n 1. This embedding of natural number arithmetic into species theory suggests that other kinds of arithmetic, logic, and computation might also be present. There is also a clear connection between the category-theoretic formulation of species as a functor category, and results relating certain such categories to topoi
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
and Cartesian closed categories
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
— connecting species theory with the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
and related systems.
Given that natural number species can be added, we immediately have a limited form of subtraction: just as the natural number system admits subtraction for certain pairs of numbers, subtraction can be defined for the corresponding species. If n and m are natural numbers with n larger than m, we can say that n 1 − m 1 is the species (n − m) 1. (If the two numbers are the same, the result is 0 — the identity for addition.) In the world of species, this makes sense because m 1 is a subspecies of n 1; likewise, knowing that E = 1 + E+, we could say that E+ = E − 1.
Going further, subtraction can be defined for all species so that the correct algebraic laws apply. Virtual species are an extension to the species concept that allow inverses to exist for addition, as well as having many other useful properties. If S is the semiring of species, then the ring V of virtual species is (S × S) / ~, where "~" is the equivalence relation
~ (H, K) if and only if F + K is isomorphic to G + H.
The equivalence class of (F, G) is written "F − G". A species F of S appears as F − 0 in V, and its additive inverse is 0 − F.
Addition of virtual species is by component:
+ (H − K) = (F + H) − (G + K).
In particular, the sum of F − 0 and 0 − F is the virtual species F − F, which is the same as 0 − 0: this is the zero of V. Multiplication is defined as·(H − K) = (F·H + G·K) − (F·K + G·H)
and its unit is 1 − 0. Together, these make V into a commutative ring, which as an algebraic structure is much easier to deal with than a semiring. Other operations carry over from species to virtual species in a very natural way, as do the associated power series. "Completing" the class of species like this also means that certain differential equations insoluble over S do have solutions in V.
Generalizations
Species need not be functors from to : other categories can replace these, to obtain species of a different nature.
- A species in k sorts is a functor
. Here, the structures produced can have elements drawn from distinct sources. - A functor to
, the category of R-weighted sets for R a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of power series, is a weighted species. - A tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
ial species is a functor into the category of finite-dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Software
Operations with species are supported by Sage and, using a special package, also by HaskellHaskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
.