
André–Quillen cohomology
Encyclopedia
In commutative algebra
, André–Quillen cohomology is a theory of cohomology
for commutative ring
s which is closely related to the cotangent complex
. It was defined independently by M. André and by Daniel Quillen using methods of homotopy theory. It comes with a parallel homology theory called André–Quillen homology.
functor DerA(B, M). Before the general definitions of André and Quillen, it was known for a long time that given morphisms of commutative rings and a C-module M, there is a three-term exact sequence
of derivation modules: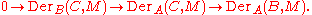
This term can be extended to a six-term exact sequence using the functor Exalcomm of extensions of commutative algebras and a nine-term exact sequence using the Lichtenbaum–Schlessinger functors. André–Quillen cohomology extends this exact sequence even further. In the zeroth degree, it is the module of derivations; in the first degree, it is Exalcomm; and in the second degree, it is the second degree Lichtenbaum–Schlessinger functor.
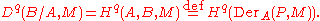
The qth André–Quillen homology group is: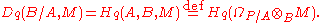
Let denote the relative cotangent complex
of B over A. Then we have the formulas:

Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, André–Quillen cohomology is a theory of cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
for commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s which is closely related to the cotangent complex
Cotangent complex
In mathematics the cotangent complex is a roughly a universal linearization of a morphism of geometric or algebraic objects. Cotangent complexes were originally defined in special cases by a number of authors. Luc Illusie, Daniel Quillen, and M...
. It was defined independently by M. André and by Daniel Quillen using methods of homotopy theory. It comes with a parallel homology theory called André–Quillen homology.
Motivation
Let A be a commutative ring, B be an A-algebra, and M be a B-module. André–Quillen cohomology is the derived functors of the derivationDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
functor DerA(B, M). Before the general definitions of André and Quillen, it was known for a long time that given morphisms of commutative rings and a C-module M, there is a three-term exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of derivation modules:
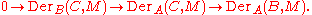
This term can be extended to a six-term exact sequence using the functor Exalcomm of extensions of commutative algebras and a nine-term exact sequence using the Lichtenbaum–Schlessinger functors. André–Quillen cohomology extends this exact sequence even further. In the zeroth degree, it is the module of derivations; in the first degree, it is Exalcomm; and in the second degree, it is the second degree Lichtenbaum–Schlessinger functor.
Definition
Let B be an A-algebra, and let M be a B-module. Let P be a simplicial cofibrant A-algebra resolution of B. André notates the qth cohomology group of B over A with coefficients in M by , while Quillen notates the same group as . The qth André–Quillen cohomology group is: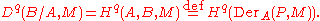
The qth André–Quillen homology group is:
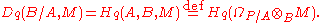
Let denote the relative cotangent complex
Cotangent complex
In mathematics the cotangent complex is a roughly a universal linearization of a morphism of geometric or algebraic objects. Cotangent complexes were originally defined in special cases by a number of authors. Luc Illusie, Daniel Quillen, and M...
of B over A. Then we have the formulas:



