Cotangent complex
Encyclopedia
In mathematics
the cotangent complex is a roughly a universal linearization of a morphism
of geometric or algebraic objects. Cotangent complexes were originally defined in special cases by a number of authors. Luc Illusie
, Daniel Quillen, and M. André independently came up with a definition that works in all cases.
and that f : X → Y is a morphism between them. The cotangent complex of f is a more universal version of the relative Kähler differentials ΩX/Y. The most basic motivation for such an object is the exact sequence of Kähler differentials associated to two morphisms. If Z is another variety, and if g : Y → Z is another morphism, then there is an exact sequence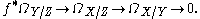
In some sense, therefore, relative Kähler differentials are a right exact functor. (Literally this is not true, however, because the category of algebraic varieties is not an abelian category
, and therefore right-exactness is not defined.) In fact, prior to the definition of the cotangent complex, there were several definitions of functors that might extend the sequence further to the left, such as the Lichtenbaum–Schlessinger functors Ti and imperfection modules. Most of these were motivated by deformation theory
.
This sequence is exact on the left if the morphism f is smooth. If Ω admitted a first derived functor
, then exactness on the left would imply that the connecting homomorphism vanished, and this would certainly be true if the first derived functor of f, whatever it was, vanished. Therefore a reasonable speculation is that the first derived functor of a smooth morphism vanishes. Furthermore, when any of the functors which extended the sequence of Kähler differentials were applied to a smooth morphism, they too vanished, which suggested that the cotangent complex of a smooth morphism might be equivalent to the Kähler differentials.
Another natural exact sequence related to Kähler differentials is the conormal exact sequence. If f is a closed immersion with ideal sheaf I, then there is an exact sequence
This is an extension of the exact sequence above: There is a new term on the left, the conormal sheaf of f, and the relative differentials ΩX/Y have vanished because a closed immersion is formally unramified. If f is the inclusion of a smooth subvariety, then this sequence is a short exact sequence. This suggests that the cotangent complex of the inclusion of a smooth variety is equivalent to the conormal sheaf shifted by one term.
of coherent sheaves
X as follows:
Berthelot proves that this definition is independent of the choice of V and that for a smoothable complete intersection morphism, this complex is perfect. Furthermore, he proves that if g : Y → Z is another smoothable complete intersection morphism and if an additional technical condition is satisfied, then there is an exact triangle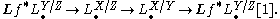
. For simplicity, we will consider only the case of simplicial commutative rings. Suppose that A and B are simplicial rings and that B is an A-algebra. Choose a resolution r : P• → B of B by simplicial free A-algebras. Applying the Kähler differential functor to P• produces a simplicial B-module. The total complex of this simplicial object is the cotangent complex LB/A. The morphism r induces a morphism from the cotangent complex to ΩB/A called the augmentation map. In the homotopy category of simplicial A-algebras (or of simplicial ringed topoi), this construction amounts to taking the left derived functor of the Kähler differential functor.
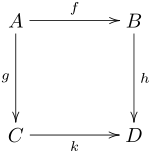
Given a commutative square as follows:
there is a morphism of cotangent complexes LB/A ⊗B D → LD/C which respects the augmentation maps. This map is constructed by choosing a free simplicial C-algebra resolution of D, say s : Q• → D. Because P• is a free object, the composite can be lifted to a morphism P• → Q•. Applying functoriality of Kähler differentials to this morphism gives the required morphism of cotangent complexes. In particular, given homomorphisms , this produces the sequence
There is a connecting homomorphism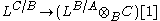
which turns this sequence into an exact triangle.
The cotangent complex can also be defined in any combinatorial model category
M. Suppose that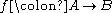
is a morphism in M. The cotangent complex 
(or 
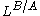) is an object in the category of spectra in 
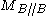. A pair of composable morphisms 
induces an exact triangle in the homotopy category,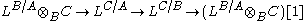 
.
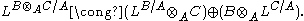
If C is a flat A-algebra, then the condition that vanishes for is automatic. The first formula then proves that the construction of the cotangent complex is local on the base in the flat topology
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the cotangent complex is a roughly a universal linearization of a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
of geometric or algebraic objects. Cotangent complexes were originally defined in special cases by a number of authors. Luc Illusie
Luc Illusie
Luc Illusie is a French mathematician. He is a former student of École Normale Supérieure, and got his PhD under the supervision of Alexander Grothendieck. He is professor emeritus at the Paris-Sud 11 University. Illusie made notable contributions to algebraic geometry.-External links:*...
, Daniel Quillen, and M. André independently came up with a definition that works in all cases.
Motivation
Suppose that X and Y are algebraic varietiesAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and that f : X → Y is a morphism between them. The cotangent complex of f is a more universal version of the relative Kähler differentials ΩX/Y. The most basic motivation for such an object is the exact sequence of Kähler differentials associated to two morphisms. If Z is another variety, and if g : Y → Z is another morphism, then there is an exact sequence
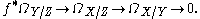
In some sense, therefore, relative Kähler differentials are a right exact functor. (Literally this is not true, however, because the category of algebraic varieties is not an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, and therefore right-exactness is not defined.) In fact, prior to the definition of the cotangent complex, there were several definitions of functors that might extend the sequence further to the left, such as the Lichtenbaum–Schlessinger functors Ti and imperfection modules. Most of these were motivated by deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
.
This sequence is exact on the left if the morphism f is smooth. If Ω admitted a first derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
, then exactness on the left would imply that the connecting homomorphism vanished, and this would certainly be true if the first derived functor of f, whatever it was, vanished. Therefore a reasonable speculation is that the first derived functor of a smooth morphism vanishes. Furthermore, when any of the functors which extended the sequence of Kähler differentials were applied to a smooth morphism, they too vanished, which suggested that the cotangent complex of a smooth morphism might be equivalent to the Kähler differentials.
Another natural exact sequence related to Kähler differentials is the conormal exact sequence. If f is a closed immersion with ideal sheaf I, then there is an exact sequence
This is an extension of the exact sequence above: There is a new term on the left, the conormal sheaf of f, and the relative differentials ΩX/Y have vanished because a closed immersion is formally unramified. If f is the inclusion of a smooth subvariety, then this sequence is a short exact sequence. This suggests that the cotangent complex of the inclusion of a smooth variety is equivalent to the conormal sheaf shifted by one term.
Early work on cotangent complexes
The cotangent complex dates back at least to SGA 6 VIII 2, where Pierre Berthelot gave a definition when f is a smoothable morphism, meaning there is a scheme V and morphisms i : X → V and h : V → Y such that f = hi, i is a closed immersion, and h is a smooth morphism. (For example, all projective morphisms are smoothable, since V can be taken to be a projective bundle over Y.) In this case, he defines the cotangent complex of f as an object in the derived categoryDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of coherent sheaves
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
X as follows:
- If J is the ideal of X in V, then
, 
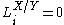for all other i,- The differential
is the pullback along i of the inclusion of J in the structure sheaf 
of V followed by the universal derivation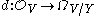 
. - All other differentials are zero.
Berthelot proves that this definition is independent of the choice of V and that for a smoothable complete intersection morphism, this complex is perfect. Furthermore, he proves that if g : Y → Z is another smoothable complete intersection morphism and if an additional technical condition is satisfied, then there is an exact triangle
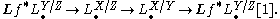
The definition of the cotangent complex
The correct definition of the cotangent complex begins in the homotopical setting. Quillen and André worked with the simplicial commutative rings, while Illusie worked with simplicial ringed topoiTopos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
. For simplicity, we will consider only the case of simplicial commutative rings. Suppose that A and B are simplicial rings and that B is an A-algebra. Choose a resolution r : P• → B of B by simplicial free A-algebras. Applying the Kähler differential functor to P• produces a simplicial B-module. The total complex of this simplicial object is the cotangent complex LB/A. The morphism r induces a morphism from the cotangent complex to ΩB/A called the augmentation map. In the homotopy category of simplicial A-algebras (or of simplicial ringed topoi), this construction amounts to taking the left derived functor of the Kähler differential functor.
Given a commutative square as follows:
there is a morphism of cotangent complexes LB/A ⊗B D → LD/C which respects the augmentation maps. This map is constructed by choosing a free simplicial C-algebra resolution of D, say s : Q• → D. Because P• is a free object, the composite can be lifted to a morphism P• → Q•. Applying functoriality of Kähler differentials to this morphism gives the required morphism of cotangent complexes. In particular, given homomorphisms , this produces the sequence
There is a connecting homomorphism
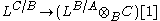which turns this sequence into an exact triangle.The cotangent complex can also be defined in any combinatorial model category
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
M. Suppose that
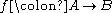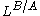is a morphism in M. The cotangent complex (or ) is an object in the category of spectra in 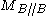. A pair of composable morphisms induces an exact triangle in the homotopy category, 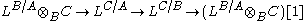.Flat base change
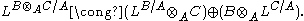
Suppose that B and C are A-algebras such that TorAq(B, C) = 0 for all . Then there are quasi-isomorphismsIf C is a flat A-algebra, then the condition that vanishes for is automatic. The first formula then proves that the construction of the cotangent complex is local on the base in the flat topology
Flat topology
In mathematics, the flat topology is a Grothendieck topology used in algebraic geometry. It is used to define the theory of flat cohomology; it also has played a fundamental role in the theory of descent...
.
Vanishing properties
Let . Then:- If B is a localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of A, then LB/A = 0. - If f is an étale morphismÉtale morphismIn algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
, then LB/A = 0. - If f is a smooth morphism, then is quasi-isomorphic to ΩB/A. In particular, it has projective dimension zero.
- If f is a local complete intersection morphism, then has projective dimension at most one.
- If A is Noetherian, B = A/I, and I is generated by a regular sequence, then
is a projective moduleProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
and LB/A is quasi-isomorphic to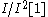
.
Examples
- Let X be smooth over S. Then the cotangent complex is ΩX/S. In Berthelot's framework, this is clear by taking V = X. In general, étale locally on S, X is a finite dimensional affine space and the morphism from X to S is projection, so we may reduce to the situation where S = Spec A and X = Spec A[x1, ..., xn]. We can take the resolution of to be the identity map, and then it is clear that the cotangent complex is the same as the Kähler differentials.
- Let X and Y be smooth over S, and assume that is a closed embedding. Using the exact triangle corresponding to the morphisms , we may determine the cotangent complex LX/Y. To do this, note that by the previous example, the cotangent complexes LX/S and LY/S consist of the Kähler differentials ΩX/S and ΩY/S in the zeroth degree, respectively, and are zero in all other degrees. The exact triangle implies that LX/Y is nonzero only in the first degree, and in that degree, it is the kernel of the map . This kernel is the conormal bundle, and the exact sequence is the conormal exact sequence, so in the first degree, LX/Y is the conormal bundle of X in Y.