
Anomalous scaling dimension
Encyclopedia
In theoretical physics
, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.
When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence
or quantum field theory
. In the latter, the anomalous scaling dimension of an operator is the contribution of quantum mechanics
to the classical scaling dimension of that operator.
The classical scaling dimension
of an operator O is determined by dimensional analysis
from the Lagrangian
(in 4 spacetime dimensions this means dimension 1 for elementary boson
ic fields including the vector potentials, 3/2 for elementary fermion
ic fields etc.). However if one computes the correlator
of two operators of this type, one often finds logarithmic divergences arising from one-loop Feynman diagram
s. The expansion in the coupling constant
has the schematic form
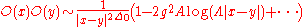
where g is a coupling constant, is the classical dimension, and
is the classical dimension, and 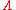 is an ultraviolet cutoff (the maximal allowed energy
is an ultraviolet cutoff (the maximal allowed energy
in the loop integrals). A is a constant that appears in the loop diagrams. The expression above may be viewed as a Taylor expansion of the full quantum dimension.

The term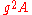 is the anomalous scaling dimension while Δ is the full dimension. Conformal field theories
is the anomalous scaling dimension while Δ is the full dimension. Conformal field theories
are typically strongly coupled and the full dimension cannot be easily calculated by Taylor expansions. The full dimensions in this case are often called critical exponent
s. These operators describe conformal bound state
s with a continuous mass spectrum.
In particular, 2Δ = d − 2 + η for the critical exponent
η for a scalar
operator. We have an anomalous scaling dimension when η ≠ 0.
An anomalous scaling dimension indicates a scale dependent wavefunction renormalization.
Anomalous scaling appears also in classical physics.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.
When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
or quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. In the latter, the anomalous scaling dimension of an operator is the contribution of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to the classical scaling dimension of that operator.
The classical scaling dimension
Classical scaling dimension
In theoretical physics, namely quantum field theory, the classical scaling dimension of an operator O is the power of mass of an operator determined by dimensional analysis from the Lagrangian...
of an operator O is determined by dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
from the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
(in 4 spacetime dimensions this means dimension 1 for elementary boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic fields including the vector potentials, 3/2 for elementary fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic fields etc.). However if one computes the correlator
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
of two operators of this type, one often finds logarithmic divergences arising from one-loop Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s. The expansion in the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
has the schematic form
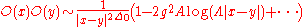
where g is a coupling constant,
 is the classical dimension, and
is the classical dimension, and 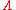 is an ultraviolet cutoff (the maximal allowed energy
is an ultraviolet cutoff (the maximal allowed energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
in the loop integrals). A is a constant that appears in the loop diagrams. The expression above may be viewed as a Taylor expansion of the full quantum dimension.

The term
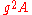 is the anomalous scaling dimension while Δ is the full dimension. Conformal field theories
is the anomalous scaling dimension while Δ is the full dimension. Conformal field theoriesConformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
are typically strongly coupled and the full dimension cannot be easily calculated by Taylor expansions. The full dimensions in this case are often called critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s. These operators describe conformal bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s with a continuous mass spectrum.
In particular, 2Δ = d − 2 + η for the critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
η for a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
operator. We have an anomalous scaling dimension when η ≠ 0.
An anomalous scaling dimension indicates a scale dependent wavefunction renormalization.
Anomalous scaling appears also in classical physics.

