
Anti-diagonal matrix
Encyclopedia
In mathematics
, an anti-diagonal matrix is a matrix
where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner (↗), known as the anti-diagonal.
More precisely, an n-by-n matrix A is an anti-diagonal matrix if the (i, j) element is zero for all i, j ∈ {1, …, n} with i + j ≠ n + 1.
An example of an anti-diagonal matrix is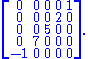
All anti-diagonal matrices are also persymmetric
.
The product of two anti-diagonal matrices is a diagonal matrix
. Furthermore, the product of an anti-diagonal matrix with a diagonal matrix is anti-diagonal, as is the product of a diagonal matrix with an anti-diagonal matrix.
An anti-diagonal matrix is invertible if and only if the entries on the diagonal from the lower left corner to the upper right corner are nonzero. The inverse of any invertible anti-diagonal matrix is also anti-diagonal, as can be seen from the paragraph above. The determinant
of an anti-diagonal matrix has absolute value
given by the product
of the entries on the diagonal from the lower left corner to the upper right corner. However, the sign of this determinant will vary because the one nonzero signed elementary product from an anti-diagonal matrix will have a different sign depending on whether the permutation
related to it is odd or even:
More precisely, the sign of the elementary product needed to calculate the determinant of an anti-diagonal matrix is related to whether the corresponding triangular number
is even or odd. This is because the number of inversions in the permutation for the only nonzero signed elementary product of any n × n anti-diagonal matrix is always equal to the nth such number.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an anti-diagonal matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner (↗), known as the anti-diagonal.
More precisely, an n-by-n matrix A is an anti-diagonal matrix if the (i, j) element is zero for all i, j ∈ {1, …, n} with i + j ≠ n + 1.
An example of an anti-diagonal matrix is
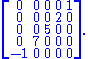
All anti-diagonal matrices are also persymmetric
Persymmetric matrix
In mathematics, persymmetric matrix may refer to:# a square matrix which is symmetric in the northeast-to-southwest diagonal; or# a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line....
.
The product of two anti-diagonal matrices is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. Furthermore, the product of an anti-diagonal matrix with a diagonal matrix is anti-diagonal, as is the product of a diagonal matrix with an anti-diagonal matrix.
An anti-diagonal matrix is invertible if and only if the entries on the diagonal from the lower left corner to the upper right corner are nonzero. The inverse of any invertible anti-diagonal matrix is also anti-diagonal, as can be seen from the paragraph above. The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of an anti-diagonal matrix has absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
given by the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of the entries on the diagonal from the lower left corner to the upper right corner. However, the sign of this determinant will vary because the one nonzero signed elementary product from an anti-diagonal matrix will have a different sign depending on whether the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
related to it is odd or even:
| Matrix size | Permutation for nonzero elementary product of anti-diagonal matrix |
Even or odd | Sign of elementary product |
|---|---|---|---|
| 2 × 2 | {2, 1} | Odd | - |
| 3 × 3 | {3, 2, 1} | Odd | - |
| 4 × 4 | {4, 3, 2, 1} | Even | + |
| 5 × 5 | {5, 4, 3, 2, 1} | Even | + |
| 6 × 6 | {6, 5, 4, 3, 2, 1} | Odd | - |
More precisely, the sign of the elementary product needed to calculate the determinant of an anti-diagonal matrix is related to whether the corresponding triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
is even or odd. This is because the number of inversions in the permutation for the only nonzero signed elementary product of any n × n anti-diagonal matrix is always equal to the nth such number.

