
Antiplane shear
Encyclopedia
Antiplane shear or antiplane strain is a special state of strain
in a body. This state of strain is achieved when the displacement
s in the body are zero in the plane of interest but nonzero in the direction perpendicular to the plane. For small strains, the strain tensor under antiplane shear can be written as
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
in a body. This state of strain is achieved when the displacement
Displacement field (mechanics)
A displacement field is an assignment of displacement vectors for all points in a region or body that is displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position...
s in the body are zero in the plane of interest but nonzero in the direction perpendicular to the plane. For small strains, the strain tensor under antiplane shear can be written as
-
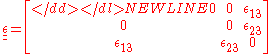
where the plane is the plane of interest and the
plane is the plane of interest and the  direction is perpendicular to that plane.
direction is perpendicular to that plane.
Displacements
The displacement field that leads to a state of antiplane shear is (in rectangular Cartesian coordinates)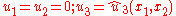
where are the displacements in the
are the displacements in the 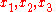 directions.
directions.
Stresses
For an isotropic, linear elastic material, the stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
tensor that results from a state of antiplane shear can be expressed as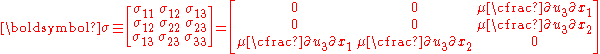
where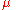 is the shear modulus of the material.
is the shear modulus of the material.
Equilibrium equation for antiplane shear
The conservation of linear momentum in the absence of inertial forces takes the form of the equilibrium equation. For general states of stress there are three equilibrium equations. However, for antiplane shear, with the assumption that body forces in the 1 and 2 directions are 0, these reduce to one equilibrium equation which is expressed as
where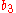 is the body force in the
is the body force in the 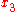 direction and
direction and 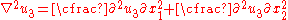 . Note that this equation is valid only for infinitesimal strains.
. Note that this equation is valid only for infinitesimal strains.
Applications
The antiplane shear assumption is used to determine the stresses and displacements due to a screw dislocation.

