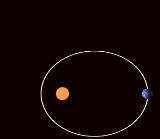
Apsidal precession
Encyclopedia
In celestial mechanics
, perihelion precession, apsidal precession or orbital precession is the precession
(rotation) of the orbit of a celestial body. More precisely it is the gradual rotation of the line joining the apsides
of an orbit, which are the points of closest and farthest approach. Perihelion is the closest point to the Sun
.
, Newton generalized his theorem to all force laws provided that the deviations from circular orbits is small, which is valid for most planets in the Solar System. However, his theorem did not account for the apsidal precession of the Moon without giving up the inverse-square law of Newton's law of universal gravitation
.
.
was noted by Urbain Le Verrier in the mid-19th century and accounted for by Einstein's
theory of general relativity
. To first approximation, this theory adds a central force that varies as the inverse fourth power of the distance.
slowly increases. Therefore the anomalistic year is slightly longer than the sidereal year. It takes about 112,000 years for the ellipse to revolve once relative to the fixed stars.
Because the anomalistic year is longer than the sidereal year while the tropical year (which calendars attempt to track) is shorter due to the precession of Earth's rotational axis, the two forms of 'precession' add. It takes about 21,000 years for the ellipse to revolve once relative to the vernal equinox, that is, for the perihelion to return to the same date (given a calendar that tracks the seasons perfectly). The dates of perihelion and of aphelion advance each year on this cycle, an average of 1 day every 58 years.
This interaction between the anomalistic and tropical cycle is important in the long-term climate variations
on Earth, called the Milankovitch cycles
. An equivalent is also known on Mars.
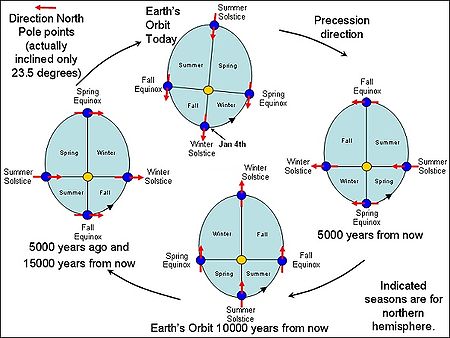
The figure illustrates the effects of precession on the northern hemisphere seasons, relative to perihelion and aphelion. Notice that the areas swept during a specific season changes through time. Orbital mechanics require that the length of the seasons be proportional to the swept areas of the seasonal quadrants, so when the orbital eccentricity
is extreme, the seasons on the far side of the orbit may be substantially longer in duration.
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, perihelion precession, apsidal precession or orbital precession is the precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
(rotation) of the orbit of a celestial body. More precisely it is the gradual rotation of the line joining the apsides
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
of an orbit, which are the points of closest and farthest approach. Perihelion is the closest point to the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
.

History
The ancient Greek astronomers noted the apsidal precession of the Moon's orbit; the precession of the solar apsides was discovered in the eleventh century by al-Zarqālī. These remained difficult to account for until the 19th century.Newton's theorem of revolving orbits
Newton derived an intriguing theorem showing that variations in the angular motion of a particle can be accounted for by the addition of a force that varies as the inverse cube of distance, without affecting the radial motion of a particle. Using a forerunner of the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, Newton generalized his theorem to all force laws provided that the deviations from circular orbits is small, which is valid for most planets in the Solar System. However, his theorem did not account for the apsidal precession of the Moon without giving up the inverse-square law of Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
.
Perturbation theory
The expected rate of apsidal precession can be calculated more accurately using the methods of perturbation theoryPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
.

General relativity
An apsidal precession of the planet MercuryMercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
was noted by Urbain Le Verrier in the mid-19th century and accounted for by Einstein's
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. To first approximation, this theory adds a central force that varies as the inverse fourth power of the distance.
Long-term climate
Because of apsidal precession the Earth's argument of periapsisArgument of periapsis
The argument of periapsis , symbolized as ω, is one of the orbital elements of an orbiting body...
slowly increases. Therefore the anomalistic year is slightly longer than the sidereal year. It takes about 112,000 years for the ellipse to revolve once relative to the fixed stars.
Because the anomalistic year is longer than the sidereal year while the tropical year (which calendars attempt to track) is shorter due to the precession of Earth's rotational axis, the two forms of 'precession' add. It takes about 21,000 years for the ellipse to revolve once relative to the vernal equinox, that is, for the perihelion to return to the same date (given a calendar that tracks the seasons perfectly). The dates of perihelion and of aphelion advance each year on this cycle, an average of 1 day every 58 years.
This interaction between the anomalistic and tropical cycle is important in the long-term climate variations
Ice age
An ice age or, more precisely, glacial age, is a generic geological period of long-term reduction in the temperature of the Earth's surface and atmosphere, resulting in the presence or expansion of continental ice sheets, polar ice sheets and alpine glaciers...
on Earth, called the Milankovitch cycles
Milankovitch cycles
Milankovitch theory describes the collective effects of changes in the Earth's movements upon its climate, named after Serbian civil engineer and mathematician Milutin Milanković, who worked on it during First World War internment...
. An equivalent is also known on Mars.
The figure illustrates the effects of precession on the northern hemisphere seasons, relative to perihelion and aphelion. Notice that the areas swept during a specific season changes through time. Orbital mechanics require that the length of the seasons be proportional to the swept areas of the seasonal quadrants, so when the orbital eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
is extreme, the seasons on the far side of the orbit may be substantially longer in duration.

