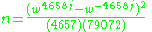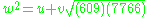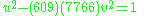Archimedes' cattle problem
Encyclopedia
Archimedes' cattle problem (or the problema bovinum or problema Archimedis) is a problem in Diophantine analysis, the study of polynomial equations with integer
solutions. Attributed to Archimedes
, the problem involves computing the number of cattle in a herd of the sun god
from a given set of restrictions. The problem was discovered by Gotthold Ephraim Lessing
in a Greek manuscript containing a poem of forty-four lines, in the Herzog August Library in Wolfenbüttel
, Germany
in 1773.
The problem remained unsolved for a number of years, due partly to the difficulty of computing the huge numbers involved in the solution. The general solution was found in 1880 by A. Amthor; he gave the exact solution using exponentials and showed that it was about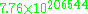
cattle. The decimal form is too long for humans to calculate exactly, but multiple precision arithmetic
packages on computers can easily write it out explicitly.
was appointed librarian of the Herzog August Library in Wolfenbüttel
, Germany
, which contained many Greek and Latin manuscripts. A few years later, Lessing published translations of some of the manuscripts with commentaries. Among them was a Greek poem of forty-four lines, containing an arithmetical problem which asks the reader to find the number of cattle in the herd of the god of the sun
. The name of Archimedes appears in the title of the poem, it being said that he sent it in a letter to Eratosthenes
to be investigated by the mathematicians of Alexandria
. The claim that Archimedes authored the poem is disputed, though, as no mention of the problem has been found in the writings of the Greek mathematicians.
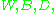and 
, and 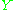the number of white, black, dappled, and yellow cows are written as 
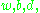and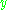 
, the problem is simply to find a solution to:
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
solutions. Attributed to Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, the problem involves computing the number of cattle in a herd of the sun god
Helios
Helios was the personification of the Sun in Greek mythology. Homer often calls him simply Titan or Hyperion, while Hesiod and the Homeric Hymn separate him as a son of the Titans Hyperion and Theia or Euryphaessa and brother of the goddesses Selene, the moon, and Eos, the dawn...
from a given set of restrictions. The problem was discovered by Gotthold Ephraim Lessing
Gotthold Ephraim Lessing
Gotthold Ephraim Lessing was a German writer, philosopher, dramatist, publicist, and art critic, and one of the most outstanding representatives of the Enlightenment era. His plays and theoretical writings substantially influenced the development of German literature...
in a Greek manuscript containing a poem of forty-four lines, in the Herzog August Library in Wolfenbüttel
Wolfenbüttel
Wolfenbüttel is a town in Lower Saxony, Germany, located on the Oker river about 13 kilometres south of Brunswick. It is the seat of the District of Wolfenbüttel and of the bishop of the Protestant Lutheran State Church of Brunswick...
, Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
in 1773.
The problem remained unsolved for a number of years, due partly to the difficulty of computing the huge numbers involved in the solution. The general solution was found in 1880 by A. Amthor; he gave the exact solution using exponentials and showed that it was about
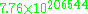cattle. The decimal form is too long for humans to calculate exactly, but multiple precision arithmeticArbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
packages on computers can easily write it out explicitly.
History
In 1769, Gotthold Ephraim LessingGotthold Ephraim Lessing
Gotthold Ephraim Lessing was a German writer, philosopher, dramatist, publicist, and art critic, and one of the most outstanding representatives of the Enlightenment era. His plays and theoretical writings substantially influenced the development of German literature...
was appointed librarian of the Herzog August Library in Wolfenbüttel
Wolfenbüttel
Wolfenbüttel is a town in Lower Saxony, Germany, located on the Oker river about 13 kilometres south of Brunswick. It is the seat of the District of Wolfenbüttel and of the bishop of the Protestant Lutheran State Church of Brunswick...
, Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
, which contained many Greek and Latin manuscripts. A few years later, Lessing published translations of some of the manuscripts with commentaries. Among them was a Greek poem of forty-four lines, containing an arithmetical problem which asks the reader to find the number of cattle in the herd of the god of the sun
The Cattle of Helios
In Greek mythology, the Cattle of Helios pastured on the island of Thrinacia, which is believed to be modern Sicily. Helios, also known as the sun god, is said to have had seven herds of oxen and seven flocks of sheep, each numbering fifty head. In the Odyssey, Homer describes this immortal cattle...
. The name of Archimedes appears in the title of the poem, it being said that he sent it in a letter to Eratosthenes
Eratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
to be investigated by the mathematicians of Alexandria
Alexandria
Alexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
. The claim that Archimedes authored the poem is disputed, though, as no mention of the problem has been found in the writings of the Greek mathematicians.
Problem
The problem, from an abridgement of the German translations published by Georg Nesselmann in 1842, and by Krumbiegel in 1880, states:
Compute, O friend, the number of the cattle of the sun which once grazed upon the plains of Sicily, divided according to color into four herds, one milk-white, one black, one dappled and one yellow. The number of bulls is greater than the number of cows, and the relations between them are as follows:
- White bulls
black bulls + yellow bulls,
- Black bulls
dappled bulls + yellow bulls,
- Dappled bulls
white bulls + yellow bulls,
- White cows
black herd,
- Black cows
dappled herd,
- Dappled cows
yellow herd,
- Yellow cows
white herd.
If thou canst give, O friend, the number of each kind of bulls and cows, thou art no novice in numbers, yet can not be regarded as of high skill. Consider, however, the following additional relations between the bulls of the sun:
- White bulls + black bulls = a square number
Square numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
,- Dappled bulls + yellow bulls = a triangular number
Triangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
.
If thou hast computed these also, O friend, and found the total number of cattle, then exult as a conqueror, for thou hast proved thyself most skilled in numbers.
Solution
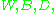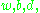The first part of the problem can be solved readily by setting up a system of equations. If the number of white, black, dappled, and yellow bulls are written as and , and the number of white, black, dappled, and yellow cows are written as and 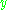, the problem is simply to find a solution to:-
which is a system of seven equations with eight unknowns. It is indeterminateIndeterminate systemAn indeterminate system is a system of simultaneous equations which has infinitely many solutions or no solutions at all. The system may be said to be underspecified.-Situations:...
, and has infinitely many solutions. The least positive integers satisfying the seven equations are:
-
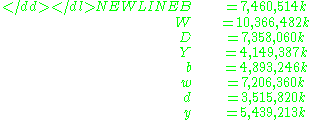
which is a total of 50,389,082k cattle and the other solutions are integral k multiples of these. Note that the first four numbers are multiples of 4657, a value which will appear repeatedly below.
The general solution to the second part of the problem was first found by A. Amthor in 1880. The following version of it was described by H. W. Lenstra , based on Pell's equationPell's equationPell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
: the solution given above for the first part of the problem should be multiplied by
where
and j is any positive integer. Equivalently, squaring w results in,
where {u,v} are the fundamental solutions of the Pell equation,
The size of the smallest herd that could satisfy both the first and second parts of the problem is then given by j = 1, and is about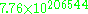
(first solved by Amthor). Modern computers can easily print out all digits of the answer. This was first done at the University of WaterlooUniversity of WaterlooThe University of Waterloo is a comprehensive public university in the city of Waterloo, Ontario, Canada. The school was founded in 1957 by Drs. Gerry Hagey and Ira G. Needles, and has since grown to an institution of more than 30,000 students, faculty, and staff...
, in 1965 by Hugh C. Williams, R. A. German, and Charles Robert Zarnke. They used a combination of the IBM 7040IBM 7040The IBM 7040 was a historic but short-lived model of transistor computer built in the 1960s.It was announced by IBM in December 1961, but did not ship until April, 1963. A later member of the IBM 700/7000 series of scientific computers, it was a scaled down version of the IBM 7090. It was not fully...
and IBM 1620IBM 1620The IBM 1620 was announced by IBM on October 21, 1959, and marketed as an inexpensive "scientific computer". After a total production of about two thousand machines, it was withdrawn on November 19, 1970...
computers.
Pell Equation
The constraints of the second part of the problem are straightforward and the actual Pell equation that needs to be solved can easily be given. First, it asks that B+W should be a squareSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, or using the values given above,
thus one should set k = (3)(11)(29)(4657)q2 for some integer q. That solves the first condition. For the second, it requires that D+Y should be a triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
,
Solving for t,
Substituting the value of D+Y and k and finding a value of q2 such that the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of this quadratic is a perfect square p2 entails solving the Pell equation,
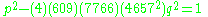
Amthor's approach discussed in the previous section was essentially to find the smallest v such that it is integrally divisible by 2*4657. The fundamental solution of this equation has more than 100,000 digits but can be solved by online software such as Dario Alpern's "Quadratic Two-Variable Equation Solver" in about 50 seconds. -
-
