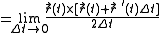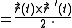Areal velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

(sector velocity, sectorial velocity) is the rate at which area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 is swept out by a particle as it moves along a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

. In many applications, the curve lies in a plane, but in others, it is a space curve.

The adjoining figure shows a continuously differentiable curve in blue. At time t, a moving particle is located at point B, and at time t + Δt the particle has moved to point C.

The area swept out during time period Δt by the particle is approximately equal to the area of triangle ABC. As Δt approaches zero this near equality becomes exact as a limit

Limit of a function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

.

The vectors AB and AC add up by the parallelogram rule to vector AD, so that point D is the fourth corner of parallelogram ABDC shown in the figure.

The area of triangle ABC (in green) is half the area of parallelogram ABDC, and the area of ABDC is equal to the magnitude of the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

 of vectors AB and AC. One may form a vector whose magnitude is the area ABCD, and which is perpendicular to the parallelogram ABCD. Then,


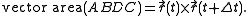
Hence,


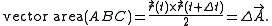
The areal velocity vector is

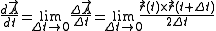
But, 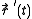is the velocity vector 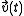of the moving particle, so that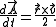

The areal velocity vector can be placed at the moving point B. As the particle moves along its path in space, it sweeps out a cone-shaped surface. The areal velocity vector is perpendicular to this surface, and, in general, varies in both magnitude and direction. In planar problems, such as the orbit of a planet about the sun, the direction of the areal velocity vector is perpendicular to the orbital plane. Kepler's second law is a statement of the constancy of the rate at which the position vector of a planet sweeps out area, with the sun taken as origin. The path of the planet is an ellipse, with the sun at one focus (Kepler's first law).

The angular momentum of the particle is



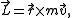
and hence
.

The direction of the angular momentum vector L is always the same as that of the areal velocity vector. Angular momentum is conserved if and only if the areal velocity is a constant vector. Thus, in the Kepler problem, the angular momentum of a planet about the sun is conserved and the areal velocity is a vector of constant magnitude perpendicular to the orbital plane. In some problems, a component of angular momentum is conserved, and in these cases, the corresponding component of areal velocity is constant. For a single particle, areal velocity provides a geometrical interpretation of angular momentum.

The concept of areal velocity is closely linked historically with the concept of angular momentum. Isaac Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

 was the first scientist to recognize the dynamical significance of Kepler's second law. With the aid of his laws of motion, he proved in 1684 that any planet that is attracted to a fixed center sweeps out equal areas in equal intervals of time. By the middle of the 18th century, the principle of angular momentum was discovered gradually by Daniel Bernoulli

Daniel Bernoulli

Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...

 and Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

 and Patrick d'Arcy

Patrick d'Arcy

Patrick d'Arcy was born in the west of Ireland. His family, who were Catholics, suffered under the penal laws. In 1739 d'Arcy was sent abroad by his parents to an uncle in Paris...

; d'Arcy's version of the principle was phrased in terms of swept area. For this reason, the principle of angular momentum was often referred to in the older literature in mechanics as "the principle of areas." Since the concept of angular momentum includes more than just geometry, the designation "principle of areas" has been dropped in modern works.