Askey–Gasper inequality
Encyclopedia
In mathematics, the Askey–Gasper inequality is an inequality for Jacobi polynomials proved by and used in the proof of the Bieberbach conjecture.
where
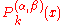
is a Jacobi polynomial.
The case when β=0 and α is a non-negative integer was used by Louis de Branges in his proof of the Bieberbach conjecture.
The inequality can also be written as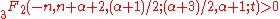
for 0≤t<1, α>–1
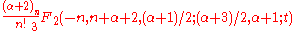
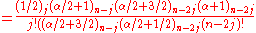
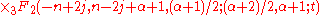
with the Clausen inequality.
.
Statement
It states that if β ≥ 0, α + β ≥ −2, and −1 ≤ x ≤ 1 thenwhere
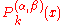
is a Jacobi polynomial.
The case when β=0 and α is a non-negative integer was used by Louis de Branges in his proof of the Bieberbach conjecture.
The inequality can also be written as
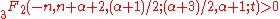for 0≤t<1, α>–1Proof
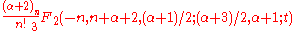
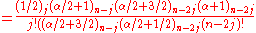
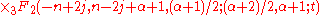
gave a short proof of this inequality, by combining the identitywith the Clausen inequality.
Generalizations
give some generalizations of the Askey–Gasper inequality to basic hypergeometric seriesBasic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
.