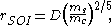Attitude dynamics and control
Encyclopedia
Spacecraft flight dynamics is the science of space vehicle performance, stability, and control. It requires analysis of the six degrees of freedom of the vehicle's flight, which are similar to those of aircraft: translation
in three dimensional axes; and its orientation
about the vehicle's center of mass in these axes, known as pitch, roll and yaw, with respect to a defined frame of reference
.
Dynamics is the modeling of the changing position and orientation of a vehicle, in response to external forces acting on the body. For a spacecraft, these forces are of three types: propulsive
force (usually provided by the vehicle's engine thrust); gravitational
force exerted by the Earth or other celestial bodies; and aerodynamic lift and drag (when flying in the atmosphere of the Earth or other body, such as Mars or Venus). The vehicle's attitude must be taken into account because of its effect on the aerodynamic and propulsive forces. There are other reasons, unrelated to flight dynamics, for controlling the vehicle's attitude in non-powered flight (e.g., thermal control, solar power generation, communications, or astronomical observation).
The principles of flight dynamics are normally used to control a spacecraft by means of an inertial navigation system
in conjunction with an attitude control system
.
's second law of motion:
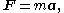
where F is the vector sum of all forces exerted on the vehicle, m is its current mass, and a is the acceleration vector, the instantaneous rate of change of velocity (v), which in turn is the instantaneous rate of change of displacement. Solving for a, acceleration equals the force sum divided by mass. Acceleration is integrated over time to get velocity, and velocity is in turn integrated to get position.
Aerodynamic forces, present near a body with significant atmosphere such as Earth
, Mars
or Venus
, are analyzed as: lift
, defined as the force compponent perpendicular to the direction of flight (not necessarily upward to balance gravity, as for an airplane); and drag
, the component parallel to, and in the opposite direction of flight. Lift and drag are modeled as the products of a coefficient times dynamic pressure acting on a reference area:
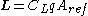
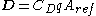
where:
The general case of a launch from Earth must take engine thrust, aerodynamic forces and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into tangential and angular components. The two equations thus become:
where θ is the flight path angle from local vertical, α is the angle of attack, F is the engine thrust, D is drag, L is lift, r is the radial distance to the planet's center, and g is the acceleration due to gravity, which varies with the inverse square of the radial distance: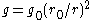
Mass, of course changes as propellant is consumed and rocket stages, engines or tanks are shed (if applicable). Integrating the two equations from time zero (when both v and θ are 0) gives planet-fixed values of v and θ at any time in the flight. Finite element analysis can be used to integrate by breaking the flight into small time increments. The trapezoidal rule can be used, approximating the output increment as the time increment times the average of the past and current values of the integrands.
For most launch vehicles, relatively small levels of lift are generated, and a gravity turn
is employed, depending mostly on the third term of the angle rate equation. But notice, when the angle is initially 0 immediately after liftoff, the only force which can cause the vehicle to pitch over is the engine thrust acting at a non-zero angle of attack (first term), until a non-zero pitch angle is attained. In the gravity turn, pitch-over is initiated by applying an increasing angle of attack (by means of gimballed engine thrust), followed by a gradual decrease in angle of attack through the remainder of the flight.
Once velocity and flight path angle are known, altitude and downrange distance are computed as:
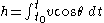
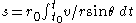
The planet-fixed values of v and θ are converted to space-fixed (inertial) values with the following conversions:
where ω is the planet's rotational rate in radians per second, φ is the launch site lattitude, and Az is the launch azimuth angle.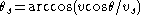
Final vs, θs and r must match the requirements of the target orbit as determined by orbital mechanics (see Orbital flight, below), where final vs is usually the required periapsis (or circular) velocity, and final θs is 90 degrees. A powered descent analysis would use the same procedure, with reverse boundary conditions.
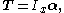
where T is the net torque
(or moment) exerted on the vehicle, Ix is its moment of inertia
about the axis of rotation, and α is the angular acceleration vector in radians per second per second. Therefore, the rotational rate in degrees per second per second is
and the angular rotation rate ω (degrees per second) is obtained by integrating α over time, and the angular rotation θ is the time integral of the rate, analogous to linear motion. The three principal moments of inertia Ix, Iy, and Iz about the roll, pitch and yaw axes, are determined through the spacecraft's center of mass.
Attitude control torque, absent aerodynamic forces, is frequently applied by a reaction control system
, a set of thrusters located about the vehicle. The thrusters are fired, either manually or under automatic guidance control, in short bursts to achieve the desired rate of rotation, and then fired in the opposite direction to halt rotation at the desired position. The torque about a specific axis is: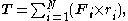
where F is the thrust of an individual thruster, and r is its distance from the center of mass (only the component of F perpendicular to r is included.)
For situations where propellant consumption may be a problem (such as long-duration satellites or space stations), alternative means may be used to provide the control torque, such as reaction wheels or control moment gyroscope
s.
This can be shown to result in the trajectory being ideally a conic section
(circle, ellipse, parabola or hyperbola) with the central body located at one focus. The parabolic trajectory represents first escape of the vehicle from the central body's gravitational field. Hyperbolic trajectories are escape trajectories with excess velocity, and will be covered under Interplanetary flight below.
Elliptical orbits are characterized by three elements. The semi-major axis a is the average of the radius at apoapsis and periapsis
:
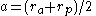
The eccentricity e may be calculated knowing the apses:
The time period for a complete orbit is dependent only on the semi-major axis, and is independent of eccentricity: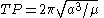
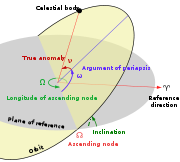The orientation of the orbit in space is specified by three angles:
The orbital plane is ideally constant, but is usually subject to small perturbations caused by planetary oblateness and the presence of other bodies.
The spacecraft's position in orbit is specified by the true anomaly, ν, an angle measured from the periapsis, or for a circular orbit, from the ascending node or reference direction. The semi-latus rectum, or radius at 90 degrees from periapsis, is: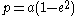
The radius at any position in flight is:
and the velocity at that position is: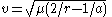
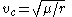
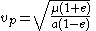
and the apoapsis velocity is: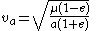
The limiting condition is a parabolic escape orbit, when e = 1 and ra becomes infinite. Escape velocity at periapsis is then
where φ is the flight path angle measured from the local horizontal (perpendicular to r.) This allows the calculation of φ, knowing radius and velocity at any point in the orbit:
Note that flight path angle is a constant 0 degrees (90 degrees from local vertical) for a circular orbit.
will enumerate various classes of maneuvers, delta-v per maneuver, number of maneuvers required over the time of the mission.
Vehicles sent on lunar or planetary missions are generally not launched on a direct trajectory, but first put into a low Earth parking orbit
; this allows the flexibility of a bigger launch window
and more time for checking that the vehicle is in good condition for the flight. A popular misconception is that escape velocity is required for flight to the Moon; it is not. Rather, the vehicle's apogee is raised high enough to take it to a point (before it reaches apogee) where it enters the Moon's gravitational sphere of influence
(though the requred velocity is close to that of escape.) This is defined as the distance from a satellite at which its gravitational pull on a spacecraft equals that of its central body, which is:
where D is the mean distance from the satellite to the central body, and
mc and ms are the masses of the central body and satellite, respectively. This value is approximately 66300 kilometres (66,300,000,000,000,000 nm) from Earth's Moon.
A significant portion of the vehicle's flight (other than immediate proximity to the Earth or Moon) requires accurate solution as a three-body problem, but may be preliminarily modeled as a patched conic.
, Apollo 10
, Apollo 11
, and Apollo 12
manned lunar missions.
Greater flexibility in lunar orbital or landing site coverage (at greater angles of lunar inclination) can be obtained by performing a plane change maneuver mid-flight; however, this takes away the free-return option, as the new plane would take the spacecraft's emergency return trajectory away from the Earth's atmospheric re-entry point, and leave the spacecraft in a high Earth orbit. This type of trajectory was used for the last five Apollo missions (13 through 17).
The excess velocity vector for a hyperbola is displaced from the periapsis tangent by a characteristic angle, therefore the periapsis injection burn must lead the planetary departure point by the same angle: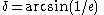
Unfortunately, the geometric equation for eccentricity of an ellipse cannot be used for a hyperbola. But the excentricity can be calculated from dynamics formulations as: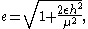
where h is the specific angular momentum as given above in Orbital flight, calculated at the periapsis: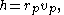
and ε is the specific energy: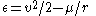
There is a great deal of variation with time of the velocity change required for a mission, because of the constantly varying relative positions of the planets. Therefore, optimum launch windows are often chosen from the results of porkchop plot
s that show contours of characteristic energy (v∞2) plotted versus departure and arrival time.
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
in three dimensional axes; and its orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
about the vehicle's center of mass in these axes, known as pitch, roll and yaw, with respect to a defined frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
.
Dynamics is the modeling of the changing position and orientation of a vehicle, in response to external forces acting on the body. For a spacecraft, these forces are of three types: propulsive
Spacecraft propulsion
Spacecraft propulsion is any method used to accelerate spacecraft and artificial satellites. There are many different methods. Each method has drawbacks and advantages, and spacecraft propulsion is an active area of research. However, most spacecraft today are propelled by forcing a gas from the...
force (usually provided by the vehicle's engine thrust); gravitational
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
force exerted by the Earth or other celestial bodies; and aerodynamic lift and drag (when flying in the atmosphere of the Earth or other body, such as Mars or Venus). The vehicle's attitude must be taken into account because of its effect on the aerodynamic and propulsive forces. There are other reasons, unrelated to flight dynamics, for controlling the vehicle's attitude in non-powered flight (e.g., thermal control, solar power generation, communications, or astronomical observation).
The principles of flight dynamics are normally used to control a spacecraft by means of an inertial navigation system
Inertial navigation system
An inertial navigation system is a navigation aid that uses a computer, motion sensors and rotation sensors to continuously calculate via dead reckoning the position, orientation, and velocity of a moving object without the need for external references...
in conjunction with an attitude control system
Attitude control system
In spaceflight, the attitude control system or attitude determination and control system of a spacecraft consists of equipment to measure, report and change the orientation of the vehicle.- Components :...
.
Basic principles
A spacecraft's flight is determined by application of NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's second law of motion:
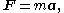
where F is the vector sum of all forces exerted on the vehicle, m is its current mass, and a is the acceleration vector, the instantaneous rate of change of velocity (v), which in turn is the instantaneous rate of change of displacement. Solving for a, acceleration equals the force sum divided by mass. Acceleration is integrated over time to get velocity, and velocity is in turn integrated to get position.
Aerodynamic forces, present near a body with significant atmosphere such as Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
or Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
, are analyzed as: lift
Lift
Lift may mean:* Lift , a mechanical force generated by an object moving through a fluid* Lift , rising air used by soaring birds and glider, hang glider and paraglider pilots for soaring flight...
, defined as the force compponent perpendicular to the direction of flight (not necessarily upward to balance gravity, as for an airplane); and drag
Drag
- In science and technology :* Drag , the force which resists motion of an object through a fluid* Drag equation, a mathematical equation used in analyzing the magnitude of drag caused by fluid flow...
, the component parallel to, and in the opposite direction of flight. Lift and drag are modeled as the products of a coefficient times dynamic pressure acting on a reference area:
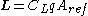
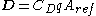
where:
- CL is roughly linear with α, the angle of attack between the vehicle axis and the direction of flight (up to a limiting value), and is 0 at α = 0 for an axisymmetric body;
- CD varies with α2;
- CL and CD vary with Reynolds number and Mach numberMach numberMach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
; - q, the dynamic pressure, is equal to 1/2 ρ v2, where ρ is atmospheric density, modeled for Earth as a function of altitude in the International Standard AtmosphereInternational Standard AtmosphereThe International Standard Atmosphere is an atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes. It has been established to provide a common reference for temperature and pressure and consists of tables of...
(using an assumed temperature distribution, hydrostatic pressure variation, and the ideal gas lawIdeal gas lawThe ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
); and - Aref is a characteristic area of the vehicle, such as cross-sectional area at the maximum diameter.
Powered flight
Flight calculations are made quite precisely for space missions, taking into account such factors as the Earth's oblateness and non-uniform mass distribution; gravitational forces of all nearby bodies, including the Moon, Sun, and other planets; and three-dimensional flight path. For preliminary studies, some simplifying assumptions can be made (spherical, uniform planet; two-body patched conic approximation; and co-planar local flight path) with reasonably small loss of accuracy.The general case of a launch from Earth must take engine thrust, aerodynamic forces and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into tangential and angular components. The two equations thus become:
where θ is the flight path angle from local vertical, α is the angle of attack, F is the engine thrust, D is drag, L is lift, r is the radial distance to the planet's center, and g is the acceleration due to gravity, which varies with the inverse square of the radial distance:
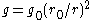
Mass, of course changes as propellant is consumed and rocket stages, engines or tanks are shed (if applicable). Integrating the two equations from time zero (when both v and θ are 0) gives planet-fixed values of v and θ at any time in the flight. Finite element analysis can be used to integrate by breaking the flight into small time increments. The trapezoidal rule can be used, approximating the output increment as the time increment times the average of the past and current values of the integrands.
For most launch vehicles, relatively small levels of lift are generated, and a gravity turn
Gravity turn
A gravity turn or zero-lift turn is a maneuver used in launching a spacecraft into, or descending from, an orbit around a celestial body such as a planet or a moon. This launch trajectory offers two main advantages over a thrust-controlled trajectory where the rocket's own thrust steers the vehicle...
is employed, depending mostly on the third term of the angle rate equation. But notice, when the angle is initially 0 immediately after liftoff, the only force which can cause the vehicle to pitch over is the engine thrust acting at a non-zero angle of attack (first term), until a non-zero pitch angle is attained. In the gravity turn, pitch-over is initiated by applying an increasing angle of attack (by means of gimballed engine thrust), followed by a gradual decrease in angle of attack through the remainder of the flight.
Once velocity and flight path angle are known, altitude and downrange distance are computed as:
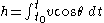
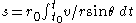
The planet-fixed values of v and θ are converted to space-fixed (inertial) values with the following conversions:
where ω is the planet's rotational rate in radians per second, φ is the launch site lattitude, and Az is the launch azimuth angle.
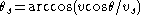
Final vs, θs and r must match the requirements of the target orbit as determined by orbital mechanics (see Orbital flight, below), where final vs is usually the required periapsis (or circular) velocity, and final θs is 90 degrees. A powered descent analysis would use the same procedure, with reverse boundary conditions.
Attitude control
Newton's second law, applied to rotational rather than linear motion, becomes: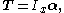where T is the net torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
(or moment) exerted on the vehicle, Ix is its moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
about the axis of rotation, and α is the angular acceleration vector in radians per second per second. Therefore, the rotational rate in degrees per second per second is
and the angular rotation rate ω (degrees per second) is obtained by integrating α over time, and the angular rotation θ is the time integral of the rate, analogous to linear motion. The three principal moments of inertia Ix, Iy, and Iz about the roll, pitch and yaw axes, are determined through the spacecraft's center of mass.
Attitude control torque, absent aerodynamic forces, is frequently applied by a reaction control system
Reaction control system
A reaction control system is a subsystem of a spacecraft whose purpose is attitude control and steering by the use of thrusters. An RCS system is capable of providing small amounts of thrust in any desired direction or combination of directions. An RCS is also capable of providing torque to allow...
, a set of thrusters located about the vehicle. The thrusters are fired, either manually or under automatic guidance control, in short bursts to achieve the desired rate of rotation, and then fired in the opposite direction to halt rotation at the desired position. The torque about a specific axis is:
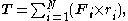
where F is the thrust of an individual thruster, and r is its distance from the center of mass (only the component of F perpendicular to r is included.)
For situations where propellant consumption may be a problem (such as long-duration satellites or space stations), alternative means may be used to provide the control torque, such as reaction wheels or control moment gyroscope
Control moment gyroscope
A control momentum gyroscope is an attitude control device generally used in spacecraft attitude control systems. A CMG consists of a spinning rotor and one or more motorized gimbals that tilt the rotor’s angular momentum. As the rotor tilts, the changing angular momentum causes a gyroscopic...
s.
Orbital flight
Orbital mechanics are used to calculate flight in orbit about a central body. For sufficiently high orbits (generally at least 100 NM in the case of Earth), aerodynamic force may be assumed to be negligible for relatively short term missions (though a small amount of drag may be present which results in decay of orbital energy over longer periods of time.) When the central body's mass is much larger than the spacecraft, and other bodies are sufficiently far away, the solution of orbital trajectories can be treated as a two-body problem.This can be shown to result in the trajectory being ideally a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
(circle, ellipse, parabola or hyperbola) with the central body located at one focus. The parabolic trajectory represents first escape of the vehicle from the central body's gravitational field. Hyperbolic trajectories are escape trajectories with excess velocity, and will be covered under Interplanetary flight below.
Elliptical orbits are characterized by three elements. The semi-major axis a is the average of the radius at apoapsis and periapsis
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
:
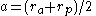
The eccentricity e may be calculated knowing the apses:
The time period for a complete orbit is dependent only on the semi-major axis, and is independent of eccentricity:
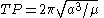
- The inclination i, of the orbital plane with the fundamental plane (this is usually a planet or moon's equatorial plane, or in the case of a solar orbit, the Earth's orbital plane around the sun, known as the eclipticEclipticThe ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
.) Positive inclination is northward, while negative inclination is southward. - The longitude of the ascending node Ω, measured in the fundamental plane counter-clockwise looking southward, from a reference direction (usually the vernal equinox) to the line where the spacecraft crosses this plane from south to north. (If inclination is zero, this angle is undefined and taken as 0.)
- The argument of periapsis ω, measured in the orbital plane counter-clockwise looking southward, from the ascending node to the periapsis. If the inclination is 0, there is no ascending node, so ω is measured from the reference direction. For a circular orbit, there is no periapsis, so ω is taken as 0.
The orbital plane is ideally constant, but is usually subject to small perturbations caused by planetary oblateness and the presence of other bodies.
The spacecraft's position in orbit is specified by the true anomaly, ν, an angle measured from the periapsis, or for a circular orbit, from the ascending node or reference direction. The semi-latus rectum, or radius at 90 degrees from periapsis, is:
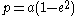
The radius at any position in flight is:
and the velocity at that position is:
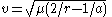
Circular orbit
For a circular orbit, ra = rp = a, and eccentricity is 0. Circular velocity at a given radius is: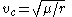Elliptical orbit
For an elliptical orbit, e is greater than 0 but less than 1. The periapsis velocity is: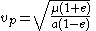and the apoapsis velocity is:
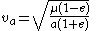
The limiting condition is a parabolic escape orbit, when e = 1 and ra becomes infinite. Escape velocity at periapsis is then
Flight path angle
The specific angular momentum of any conic orbit, h, is constant, and is equal to the product of radius and velocity at periapsis. At any other point in the orbit, it is equal to:where φ is the flight path angle measured from the local horizontal (perpendicular to r.) This allows the calculation of φ, knowing radius and velocity at any point in the orbit:
Note that flight path angle is a constant 0 degrees (90 degrees from local vertical) for a circular orbit.
True anomaly as a function of time
It can be shown that the angular momentum equation given above also relates the rate of change in true anomaly to r, v and φ, thus the true anomaly can be found as a function of time since periapsis passage by integration:Change of plane
Sample delta-v budgetDelta-v budget
In the astrodynamics and aerospace industry, a delta-v budget is the estimated delta-v requirements for the various propulsive tasks and orbital maneuvers over one or more phases of a space mission.Sample delta-v budget will enumerate various classes of maneuvers, delta-v per maneuver, number of...
will enumerate various classes of maneuvers, delta-v per maneuver, number of maneuvers required over the time of the mission.
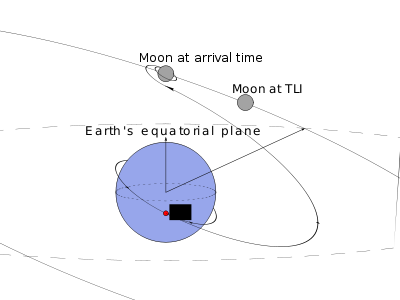
Translunar flight
Low Earth orbit
A low Earth orbit is generally defined as an orbit within the locus extending from the Earth’s surface up to an altitude of 2,000 km...
; this allows the flexibility of a bigger launch window
Launch window
Launch window is a term used in spaceflight to describe a time period in which a particular launch vehicle must be launched. If the rocket does not launch within the "window", it has to wait for the next window....
and more time for checking that the vehicle is in good condition for the flight. A popular misconception is that escape velocity is required for flight to the Moon; it is not. Rather, the vehicle's apogee is raised high enough to take it to a point (before it reaches apogee) where it enters the Moon's gravitational sphere of influence
Sphere of influence (astrodynamics)
A sphere of influence in astrodynamics and astronomy is the spherical region around a celestial body where the primary gravitational influence on an orbiting object is that body...
(though the requred velocity is close to that of escape.) This is defined as the distance from a satellite at which its gravitational pull on a spacecraft equals that of its central body, which is:
where D is the mean distance from the satellite to the central body, and
mc and ms are the masses of the central body and satellite, respectively. This value is approximately 66300 kilometres (66,300,000,000,000,000 nm) from Earth's Moon.
A significant portion of the vehicle's flight (other than immediate proximity to the Earth or Moon) requires accurate solution as a three-body problem, but may be preliminarily modeled as a patched conic.
Translunar injection
This must be timed so that the Moon will be in position to capture the vehicle, and might be modeled to a first approximation as a Hohmann transfer. 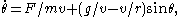However, the rocket burn duration is usually long enough, and occurs during the change in flight path angle, so that this is not very accurate, requiring instead integration of a simplified version of the velocity and angle rate equations given above in Powered flight:Mid-course corrections
A simple lunar trajectory stays in one plane, resulting in lunar flyby or orbit within a small range of inclination to the Moon's equator. This also permits a "free return", in which the spacecraft would return to the appropriate position for reentry into the Earth's atmosphere if it were not injected into lunar orbit. Relatively small velocity changes are usually required to correct for trajectory errors. Such a trajectory was used for the Apollo 8Apollo 8
Apollo 8, the second manned mission in the American Apollo space program, was the first human spaceflight to leave Earth orbit; the first to be captured by and escape from the gravitational field of another celestial body; and the first crewed voyage to return to Earth from another celestial...
, Apollo 10
Apollo 10
Apollo 10 was the fourth manned mission in the American Apollo space program. It was an F type mission—its purpose was to be a "dry run" for the Apollo 11 mission, testing all of the procedures and components of a Moon landing without actually landing on the Moon itself. The mission included the...
, Apollo 11
Apollo 11
In early 1969, Bill Anders accepted a job with the National Space Council effective in August 1969 and announced his retirement as an astronaut. At that point Ken Mattingly was moved from the support crew into parallel training with Anders as backup Command Module Pilot in case Apollo 11 was...
, and Apollo 12
Apollo 12
Apollo 12 was the sixth manned flight in the American Apollo program and the second to land on the Moon . It was launched on November 14, 1969 from the Kennedy Space Center, Florida, four months after Apollo 11. Mission commander Charles "Pete" Conrad and Lunar Module Pilot Alan L...
manned lunar missions.
Greater flexibility in lunar orbital or landing site coverage (at greater angles of lunar inclination) can be obtained by performing a plane change maneuver mid-flight; however, this takes away the free-return option, as the new plane would take the spacecraft's emergency return trajectory away from the Earth's atmospheric re-entry point, and leave the spacecraft in a high Earth orbit. This type of trajectory was used for the last five Apollo missions (13 through 17).
Interplanetary flight
In order to completely leave one planet's gravitational field to reach another, a hyperbolic trajectory relative to the departure planet is necessary, with excess velocity added to (or subracted from) the departure planet's orbital velocity around the Sun. The desired heliocentric transfer orbit to an outer planet will have its perihelion at the departure planet, requiring the hyperbolic excess velocity to be applied in the posigrade direction, when the spacecraft is away from the Sun. To an inner destination planet, aphelion will be at the departure planet, and the excess velocity is applied in the retrograde direction when the spacecraft is toward the Sun. Once the required excess velocity v∞ (sometimes called characteristic velocity) is determined, the injection velocity at periapsis for a hyperbola is:The excess velocity vector for a hyperbola is displaced from the periapsis tangent by a characteristic angle, therefore the periapsis injection burn must lead the planetary departure point by the same angle:
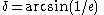
Unfortunately, the geometric equation for eccentricity of an ellipse cannot be used for a hyperbola. But the excentricity can be calculated from dynamics formulations as:
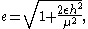
where h is the specific angular momentum as given above in Orbital flight, calculated at the periapsis:
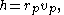
and ε is the specific energy:
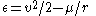
There is a great deal of variation with time of the velocity change required for a mission, because of the constantly varying relative positions of the planets. Therefore, optimum launch windows are often chosen from the results of porkchop plot
Porkchop plot
Porkchop plot is a chart that shows contours of equal characteristic energy against combinations of launch date and arrival date for a particular interplanetary flight....
s that show contours of characteristic energy (v∞2) plotted versus departure and arrival time.