
Aubin-Lions lemma
Encyclopedia
In mathematics
, the Aubin–Lions lemma is a result in the theory of Sobolev space
s of Banach space
-valued functions. More precisely, it is a compactness
criterion that is very useful in the study of nonlinear evolutionary partial differential equation
s. The result is named after the French
mathematician
s Thierry Aubin
and Jacques-Louis Lions
.
in X and that X is continuously embedded
in X1; suppose also that X0 and X1 are reflexive space
s. For 1 < p, q < +∞, let
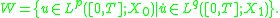
Then the embedding of W into Lp([0, T]; X) is also compact
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Aubin–Lions lemma is a result in the theory of Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
-valued functions. More precisely, it is a compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
criterion that is very useful in the study of nonlinear evolutionary partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. The result is named after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Thierry Aubin
Thierry Aubin
Thierry Aubin was a French mathematician at Centre de Mathématiques de Jussieu who worked on Riemannian geometryand non-linear partial differential equations...
and Jacques-Louis Lions
Jacques-Louis Lions
Jacques-Louis Lions ForMemRS was a French mathematician who made contributions to the theory of partial differential equations and to stochastic control, among other areas. He received the SIAM's John Von Neumann prize in 1986. Lions is listed as an ISI highly cited researcher.-Biography:After...
.
Statement of the lemma
Let X0, X and X1 be three Banach spaces with X0 ⊆ X ⊆ X1. Suppose that X0 is compactly embeddedCompactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in X and that X is continuously embedded
Continuously embedded
In mathematics, one normed vector space is said to be continuously embedded in another normed vector space if the inclusion function between them is continuous. In some sense, the two norms are "almost equivalent", even though they are not both defined on the same space...
in X1; suppose also that X0 and X1 are reflexive space
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
s. For 1 < p, q < +∞, let
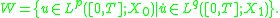
Then the embedding of W into Lp([0, T]; X) is also compact

