
BF model
Encyclopedia
The BF model is a topological field theory, which when quantized
, becomes a topological quantum field theory
. BF stands for background field. B and F, as can be seen below, are also the variables appearing in the Lagrangian
of the theory, which is helpful as a mnemonic device.
We have a 4-dimensional differentiable manifold
M, a gauge group G, which has as "dynamical" fields a two-form
B taking values in the adjoint representation
of G, and a connection form
A for G.
The action
is given by
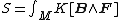
where K is an invariant nondegenerate bilinear form over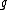 (if G is semisimple
(if G is semisimple
, the Killing form
will do) and F is the curvature form
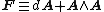
This action is diffeomorphically
invariant and gauge invariant. Its Euler-Lagrange equation
s are
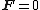 (no curvature)
(no curvature)
and
 (the covariant exterior derivative of B is zero).
(the covariant exterior derivative of B is zero).
In fact, it is always possible to gauge away any local degrees of freedom, which is why it is called a topological field theory.
However, if M is topologically nontrivial, A and B can have nontrivial solutions globally.
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
, becomes a topological quantum field theory
Topological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
. BF stands for background field. B and F, as can be seen below, are also the variables appearing in the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
of the theory, which is helpful as a mnemonic device.
We have a 4-dimensional differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M, a gauge group G, which has as "dynamical" fields a two-form
Two-form
In linear algebra, a two-form is another term for a bilinear form, typically used in informal discussions, or sometimes to indicate that the bilinear form is skew-symmetric....
B taking values in the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of G, and a connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
A for G.
The action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is given by
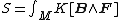
where K is an invariant nondegenerate bilinear form over
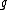 (if G is semisimple
(if G is semisimpleSemisimple
In mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
, the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
will do) and F is the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
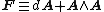
This action is diffeomorphically
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
invariant and gauge invariant. Its Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s are
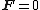 (no curvature)
(no curvature)and
 (the covariant exterior derivative of B is zero).
(the covariant exterior derivative of B is zero).In fact, it is always possible to gauge away any local degrees of freedom, which is why it is called a topological field theory.
However, if M is topologically nontrivial, A and B can have nontrivial solutions globally.

