BLS (Cryptography)
Encyclopedia
In cryptography
, the Boneh–Lynn–Shacham signature scheme allows a user to verify that a signer is authentic. The scheme uses a pairing function
for verification and signatures are group elements in some elliptic curve
. Working in an elliptic curve provides defense against index calculus attacks against allowing shorter signatures than FDH
signatures. Signatures are often referred to as short signatures, BLS short signatures, or simply BLS signatures. The signature scheme is provably secure (that is, the scheme is existentially unforgeable under adaptive chosen-message attacks) assuming both the existence of random oracle
s and the intractability of the computational Diffie–Hellman problem.
s permit such groups.
Let
be a non-degenerate, efficiently computable, bilinear pairing function
where
, 
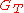are groups of prime order, 
. Let 
be a generator of 
. Consider an instance of the CDH problem,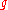 
,
, 
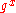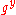. Intuitively, the pairing function 
does not help us compute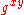 
, the solution to the CDH problem. It is conjectured that this instance of the CDH problem is intractable. Given 
, we may check to see if 
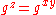without knowledge of 
, 
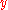, and 
, by testing whether 
holds.
By using the bilinear property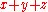
times, we see that if 
, then since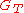 
is a prime order group, 
.
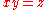in the interval [0, r − 1]. The private key is 
. The holder of the private key publishes the public key, 
.
, and some message 
, we compute the signature by hashing the bitstring 
, as 
. We output the signature 
.
and a public key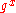 
, we verify that 
.
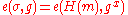Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, the Boneh–Lynn–Shacham signature scheme allows a user to verify that a signer is authentic. The scheme uses a pairing function
Pairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
for verification and signatures are group elements in some elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
. Working in an elliptic curve provides defense against index calculus attacks against allowing shorter signatures than FDH
Full Domain Hash
In cryptography, the Full Domain Hash is an RSA-based signature scheme that follows the hash-and-sign paradigm. It is provably secure in the random oracle model...
signatures. Signatures are often referred to as short signatures, BLS short signatures, or simply BLS signatures. The signature scheme is provably secure (that is, the scheme is existentially unforgeable under adaptive chosen-message attacks) assuming both the existence of random oracle
Random oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
s and the intractability of the computational Diffie–Hellman problem.
Pairing functions
A gap group is a group in which the computational Diffie–Hellman problem is intractable but the decisional Diffie–Hellman problem can be efficiently solved. Non-degenerate, efficiently computable, bilinear pairing functionPairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
s permit such groups.
Let
be a non-degenerate, efficiently computable, bilinear pairing functionPairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
where
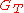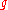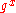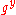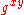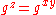, are groups of prime order, . Let be a generator of . Consider an instance of the CDH problem, ,, . Intuitively, the pairing function does not help us compute , the solution to the CDH problem. It is conjectured that this instance of the CDH problem is intractable. Given , we may check to see if without knowledge of , , 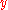and , by testing whether holds.By using the bilinear property
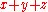times, we see that if , then since 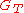is a prime order group, 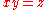.The scheme
A signature scheme consists of three functions, generate, sign, and verifyKey generation
The key generation algorithm selects a random integer in the interval [0, r − 1]. The private key is . The holder of the private key publishes the public key, .Signing
Given the private key, and some message , we compute the signature by hashing the bitstring , as . We output the signature .Verification
Given a signature and a public key 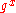, we verify that .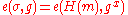