Bairstow's method
Encyclopedia
In numerical analysis
, Bairstow's method is an efficient algorithm
for finding the roots of a real polynomial
of arbitrary degree. The algorithm first appeared in the appendix of the 1920 book "Applied Aerodynamics" by Leonard Bairstow
. The algorithm finds the roots in complex conjugate
pairs using only real arithmetic.
See root-finding algorithm
for other algorithms.
to adjust the coefficients u and v in the quadratic
until its roots are also roots of the polynomial being solved. The roots of the quadratic may then be determined, and the polynomial may be divided by the quadratic to eliminate those roots. This process is then iterated until the polynomial becomes quadratic or linear, and all the roots have been determined.
Long division
of the polynomial to be solved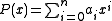
by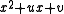
yields a quotient 
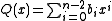and a remainder 
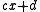such that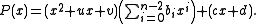
A second division of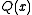
by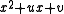 
is performed to yield a quotient 
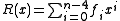and remainder 
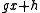with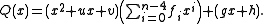
The variables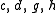
, and the 
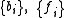are functions of 
and 
. They can be found recursively as follows.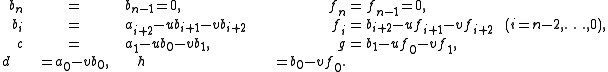
The quadratic evenly divides the polynomial when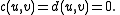
Values of
and 
for which this occurs can be discovered by picking starting values and iterating Newton's method in two dimensions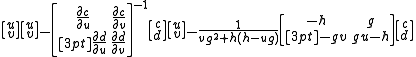
until convergence occurs. This method to find the zeroes of polynomials can thus be easily implemented with a programming language or even a spreadsheet.
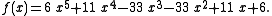
As first quadratic polynomial one may choose the normalized polynomial formed from the leading three coefficients of f(x),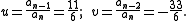
The iteration then produces the table
After eight iterations the method produced a quadratic factor that contains the roots -1/3 and -3 within the represented precision. The step length from the fourth iteration on demonstrates the superlinear speed of convergence.
The images represent pairs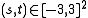
. Points in the upper half plane t>0 correspond to a linear factor with roots 
, that is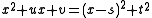 
. Points in the lower half plane t<0 correspond to quadratic factors with roots 
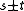, that is, 
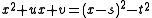, so in general 
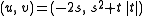. Points are colored according to the final point of the Bairstow iteration, black points indicate divergent behavior.
The first image is a demonstration of the single real root case. The second indicates that one can remedy the divergent behavior by introducing an additional real root, at the cost of slowing down the speed of convergence. The third image corresponds to the example above.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Bairstow's method is an efficient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for finding the roots of a real polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of arbitrary degree. The algorithm first appeared in the appendix of the 1920 book "Applied Aerodynamics" by Leonard Bairstow
Leonard Bairstow
Sir Leonard Bairstow, CBE, FRS, FRAeS was a son of Uriah Bairstow, a wealthy Halifax, West Yorkshire man and keen mathematician. Born in 1880 in Halifax, Bairstow is best remembered for his work in aviation and for Bairstow's method for arbitrarily finding the roots of polynomials.As a boy,...
. The algorithm finds the roots in complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
pairs using only real arithmetic.
See root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
for other algorithms.
Description of the method
Bairstow's approach is to use Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to adjust the coefficients u and v in the quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
until its roots are also roots of the polynomial being solved. The roots of the quadratic may then be determined, and the polynomial may be divided by the quadratic to eliminate those roots. This process is then iterated until the polynomial becomes quadratic or linear, and all the roots have been determined.Long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
of the polynomial to be solved
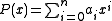
by
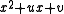yields a quotient and a remainder such thatA second division of
by 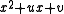is performed to yield a quotient 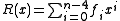and remainder with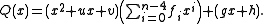The variables
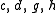, and the 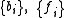are functions of and . They can be found recursively as follows.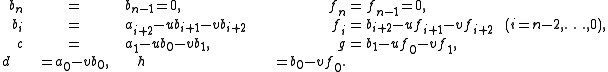The quadratic evenly divides the polynomial when
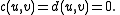
Values of
and for which this occurs can be discovered by picking starting values and iterating Newton's method in two dimensions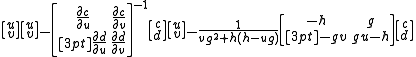until convergence occurs. This method to find the zeroes of polynomials can thus be easily implemented with a programming language or even a spreadsheet.
Example
The task is to determine a pair of roots of the polynomial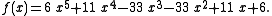As first quadratic polynomial one may choose the normalized polynomial formed from the leading three coefficients of f(x),
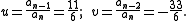
The iteration then produces the table
| Nr | u | v | step length | roots |
|---|---|---|---|---|
| 0 | 1.833333333333 | -5.500000000000 | 5.579008780071 | -0.916666666667±2.517990821623 |
| 1 | 2.979026068546 | -0.039896784438 | 2.048558558641 | -1.489513034273±1.502845921479 |
| 2 | 3.635306053091 | 1.900693009946 | 1.799922838287 | -1.817653026545±1.184554563945 |
| 3 | 3.064938039761 | 0.193530875538 | 1.256481376254 | -1.532469019881±1.467968126819 |
| 4 | 3.461834191232 | 1.385679731101 | 0.428931413521 | -1.730917095616±1.269013105052 |
| 5 | 3.326244386565 | 0.978742927192 | 0.022431883898 | -1.663122193282±1.336874153612 |
| 6 | 3.333340909351 | 1.000022701147 | 0.000023931927 | -1.666670454676±1.333329555414 |
| 7 | 3.333333333340 | 1.000000000020 | 0.000000000021 | -1.666666666670±1.333333333330 |
| 8 | 3.333333333333 | 1.000000000000 | 0.000000000000 | -1.666666666667±1.333333333333 |
After eight iterations the method produced a quadratic factor that contains the roots -1/3 and -3 within the represented precision. The step length from the fourth iteration on demonstrates the superlinear speed of convergence.
Performance
Bairstow's algorithm inherits the local quadratic convergence of Newton's method, except in the case of quadratic factors of multiplicity higher than 1, when convergence to that factor is linear. A particular kind of instability is observed when the polynomial has odd degree and only one real root. Quadratic factors that have a small value at this real root tend to diverge to infinity. |
 |
 |
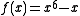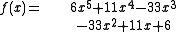The images represent pairs
. Points in the upper half plane t>0 correspond to a linear factor with roots , that is 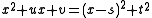. Points in the lower half plane t<0 correspond to quadratic factors with roots 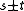, that is, 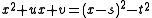, so in general 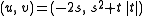. Points are colored according to the final point of the Bairstow iteration, black points indicate divergent behavior.The first image is a demonstration of the single real root case. The second indicates that one can remedy the divergent behavior by introducing an additional real root, at the cost of slowing down the speed of convergence. The third image corresponds to the example above.