Barnes integral
Encyclopedia
In mathematics, a Barnes integral or Mellin
–Barnes integral is a contour integral involving a product of gamma function
s. They were introduced by . They are closely related to generalized hypergeometric series.
The integral is usually taken along a contour which is a deformation of the imaginary axis passing to the left of all poles of factors of the form Γ(a + s) and to the right of all poles of factors of the form Γ(a − s).
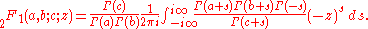
This equality can be obtained by moving the contour to the right while picking up the residues
at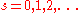
. Given proper convergence conditions, one can relate more general Barnes' integrals and hypergeometric functions 
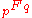in a similar way.
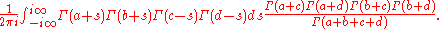
This is an analogue of Gauss's 2F1 summation formula, and also an extension of Euler's beta integral. The integral in it is sometimes called Barnes's beta integral.
The second Barnes lemma states
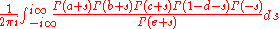
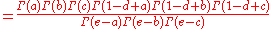
where e = a + b + c − d + 1. This is an analogue of Saalschütz's summation formula.
, and many of the other results can also be extended to this case .
Hjalmar Mellin
Robert Hjalmar Mellin was a Finnish mathematician and functional theorist.He studied at the University of Helsinki and later in Berlin under Karl Weierstrass. He is most noted as the developer of the integral transform known as the Mellin transform...
–Barnes integral is a contour integral involving a product of gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
s. They were introduced by . They are closely related to generalized hypergeometric series.
The integral is usually taken along a contour which is a deformation of the imaginary axis passing to the left of all poles of factors of the form Γ(a + s) and to the right of all poles of factors of the form Γ(a − s).
Hypergeometric series
The hypergeometric function is given as a Barnes integral by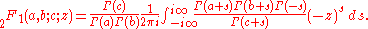This equality can be obtained by moving the contour to the right while picking up the residues
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
at
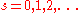. Given proper convergence conditions, one can relate more general Barnes' integrals and hypergeometric functions 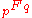in a similar way.Barnes lemmas
The first Barnes lemma states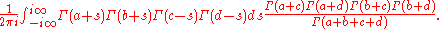This is an analogue of Gauss's 2F1 summation formula, and also an extension of Euler's beta integral. The integral in it is sometimes called Barnes's beta integral.
The second Barnes lemma states
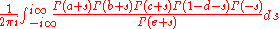
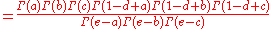
where e = a + b + c − d + 1. This is an analogue of Saalschütz's summation formula.
q-Barnes integrals
There are analogues of Barnes integrals for basic hypergeometric seriesBasic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
, and many of the other results can also be extended to this case .