
Barrett reduction
Encyclopedia
In modular arithmetic
, Barrett reduction is a reduction algorithm
introduced in 1986 by P.D. Barrett. A naive way of computing
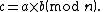
would be to use a fast division algorithm
. Barrett reduction and Montgomery reduction
are algorithms designed to optimize this operation.
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, Barrett reduction is a reduction algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
introduced in 1986 by P.D. Barrett. A naive way of computing
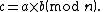
would be to use a fast division algorithm
Division algorithm
In mathematics, and more particularly in arithmetic, the usual process of division of integers producing a quotient and a remainder can be specified precisely by a theorem stating that these exist uniquely with given properties. An integer division algorithm is any effective method for producing...
. Barrett reduction and Montgomery reduction
Montgomery reduction
In arithmetic computation, Montgomery reduction is an algorithm introduced in 1985 by Peter Montgomery that allows modular arithmetic to be performed efficiently when the modulus is large ....
are algorithms designed to optimize this operation.
Sources
- P.D. Barrett, "Implementing the Rivest Shamir and Adleman Public Key Encryption Algorithm on a Standard Digital Signal Processor," Advances in Cryptology — CRYPTO'86, Springer, 1986. http://www.springerlink.com/content/c4f3rqbt5dxxyad4/
- Chapter 14 of Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone. Handbook of Applied Cryptography. CRC Press, 1996. ISBN 0-8493-8523-7.
- Bosselaers, et al., "Comparison of Three Modular Reduction Functions," Advances in Cryptology-Crypto'93, 1993. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.40.3779

