Bartlett's bisection theorem
Encyclopedia
Bartlett's Bisection Theorem is an electrical theorem
in network analysis
due to Albert Charles Bartlett
. The theorem shows that any symmetrical two-port network
can be transformed into a lattice network. The theorem often appears in filter theory where the lattice network is sometimes known as a filter X-section following the common filter theory practice of naming sections after alphabetic letters to which they bear a resemblance.
The theorem as originally stated by Bartlett required the two halves of the network to be topologically symmetrical. The theorem was later extended by Wilhelm Cauer
to apply to all networks which were electrically symmetrical. That is, the physical implementation of the network is not of any relevance. It is only required that its response in both halves are symmetrical.
s) than other designs. Ladder topology is much more popular. However, they do have the property of being intrinsically balanced and a balanced version of another topology
, such as T-sections, may actually end up using more inductors. One application is for all-pass
phase correction filters on balanced telecommunication lines. The theorem also makes an appearance in the design of crystal filters at RF frequencies. Here ladder topologies have some undesirable properties, but a common design strategy is to start from a ladder implementation because of its simplicity. Bartlett's theorem is then used to transform the design to an intermediate stage as a step towards the final implementation (using a transformer to produce an unbalanced version of the lattice topology).
.
Now consider the network N with two identical voltage generators connected to the ports but with opposite polarity. Just as superposition
of currents through the branches at the plane of symmetry must be zero in the previous case, by analogy and applying the principle of duality, superposition of voltages between nodes
at the plane of symmetry must likewise be zero in this case. The input impedance is thus the same as the short circuit impedance of ½N. Let us call that impedance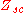
.
Bartlett's bisection theorem states that the network N is equivalent to a lattice network with series branches of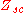
and cross branches of 
.
. Those branches can thus be removed and left open circuit without any effect on the rest of the circuit. This leaves a circuit loop with a voltage of 2E and an impedance of 
giving a current in the loop of;
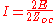
and an input impedance of;
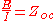
as it is required to be for equivalence to the original two-port.
Similarly, reversing one of the generators results, by an identical argument, in a loop with an impedance of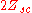
and an input impedance of;
Recalling that these generator configurations are the precise way in which
and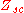 
were defined in the original two-port it is proved that the lattice is equivalent for those two cases. It is proved that this is so for all cases by considering that all other input and output conditions can be expressed as a linear superposition of the two cases already proved.
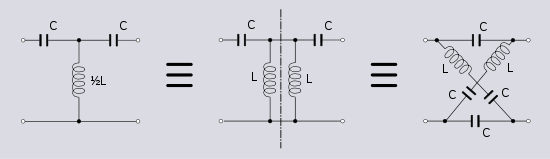
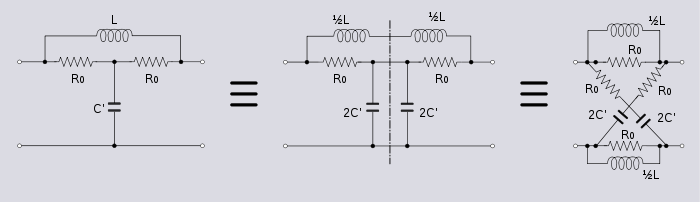It is possible to use the Bartlett transformation in reverse; that is, to transform a symmetrical lattice network into some other symmetrical topology. The examples shown above could just as equally have been shown in reverse. However, unlike the examples above, the result is not always physically realisable with linear passive components. This is because there is a possibility the reverse transform will generate components with negative values. Negative quantities can only be physically realised with active components present in the network.
There is an extension to Bartlett's theorem that allows a symmetrical filter
network operating between equal input and output impedance terminations to be modified for unequal source and load impedances. This is an example of impedance scaling of a prototype filter
. The symmetrical network is bisected along its plane of symmetry. One half is impedance-scaled to the input impedance and the other is scaled to the output impedance. The response shape of the filter remains the same. This does not amount to an impedance matching
network, the impedances looking in to the network ports bear no relationship to the termination impedances. This means that a network designed by Bartlett's theorem, while having exactly the filter response predicted, also adds a constant attenuation in addition to the filter response. In impedance matching networks, a usual design criteria is to maximise power transfer. The output response is "the same shape" relative to the voltage of the theoretical ideal generator driving the input. It is not the same relative to the actual input voltage which is delivered by the theoretical ideal generator via its load impedance.
The constant gain due to the difference in input and output impedances is given by;
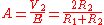
Note that it is possible for this to be greater than unity, that is, a voltage gain is possible, but power is always lost.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in network analysis
Network analysis (electrical circuits)
A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
due to Albert Charles Bartlett
Albert Charles Bartlett
Albert Charles Bartlett was an electrical engineer working for the General Electric Company in Wembley. He had some correspondence with Wilhelm Cauer on the subject of filter designs....
. The theorem shows that any symmetrical two-port network
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
can be transformed into a lattice network. The theorem often appears in filter theory where the lattice network is sometimes known as a filter X-section following the common filter theory practice of naming sections after alphabetic letters to which they bear a resemblance.
The theorem as originally stated by Bartlett required the two halves of the network to be topologically symmetrical. The theorem was later extended by Wilhelm Cauer
Wilhelm Cauer
Wilhelm Cauer was a German mathematician and scientist. He is most noted for his work on the analysis and synthesis of electrical filters and his work marked the beginning of the field of network synthesis...
to apply to all networks which were electrically symmetrical. That is, the physical implementation of the network is not of any relevance. It is only required that its response in both halves are symmetrical.
Applications
Lattice topology filters are not very common. The reason for this is that they require more components (especially inductorInductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
s) than other designs. Ladder topology is much more popular. However, they do have the property of being intrinsically balanced and a balanced version of another topology
Topology (electronics)
The topology of an electronic circuit is the form taken by the network of interconnections of the circuit components. Different specific values or ratings of the components are regarded as being the same topology....
, such as T-sections, may actually end up using more inductors. One application is for all-pass
All-pass filter
An all-pass filter is a signal processing filter that passes all frequencies equally, but changes the phase relationship between various frequencies. It does this by varying its propagation delay with frequency...
phase correction filters on balanced telecommunication lines. The theorem also makes an appearance in the design of crystal filters at RF frequencies. Here ladder topologies have some undesirable properties, but a common design strategy is to start from a ladder implementation because of its simplicity. Bartlett's theorem is then used to transform the design to an intermediate stage as a step towards the final implementation (using a transformer to produce an unbalanced version of the lattice topology).
Definition
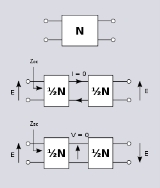
Start with a two-port network, N, with a plane of symmetry between the two ports. Next cut N through its plane of symmetry to form two new identical two-ports, ½N. Connect two identical voltage generators to the two ports of N. It is clear from the symmetry that no current is going to flow through any branch passing through the plane of symmetry. The impedance measured into a port of N under these circumstances will be the same as the impedance measured if all the branches passing through the plane of symmetry were open circuit. It is therefore the same impedance as the open circuit impedance of ½N. Let us call that impedance.Now consider the network N with two identical voltage generators connected to the ports but with opposite polarity. Just as superposition
Superposition theorem
The superposition theorem for electrical circuits states that the response in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, while all other independent sources are replaced...
of currents through the branches at the plane of symmetry must be zero in the previous case, by analogy and applying the principle of duality, superposition of voltages between nodes
Node (circuits)
In electrical engineering, node refers to any point on a circuit where two or more circuit elements meet. For two nodes to be different, their voltages must be different. Without any further knowledge, it is easy to establish how to find a node by using Ohm's Law: V=IR. When looking at circuit...
at the plane of symmetry must likewise be zero in this case. The input impedance is thus the same as the short circuit impedance of ½N. Let us call that impedance
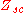.Bartlett's bisection theorem states that the network N is equivalent to a lattice network with series branches of
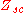and cross branches of .Proof
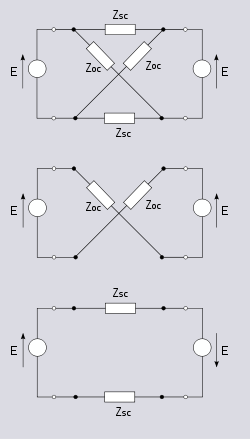
Consider the lattice network shown with identical generators, E, connected to each port. It is clear from symmetry and superposition that no current is flowing in the series branches. Those branches can thus be removed and left open circuit without any effect on the rest of the circuit. This leaves a circuit loop with a voltage of 2E and an impedance of giving a current in the loop of;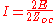and an input impedance of;
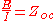
as it is required to be for equivalence to the original two-port.
Similarly, reversing one of the generators results, by an identical argument, in a loop with an impedance of
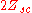and an input impedance of;Recalling that these generator configurations are the precise way in which
and 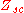were defined in the original two-port it is proved that the lattice is equivalent for those two cases. It is proved that this is so for all cases by considering that all other input and output conditions can be expressed as a linear superposition of the two cases already proved.Examples
Extension of the theorem
Electronic filter
Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
network operating between equal input and output impedance terminations to be modified for unequal source and load impedances. This is an example of impedance scaling of a prototype filter
Prototype filter
Prototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regards to...
. The symmetrical network is bisected along its plane of symmetry. One half is impedance-scaled to the input impedance and the other is scaled to the output impedance. The response shape of the filter remains the same. This does not amount to an impedance matching
Impedance matching
In electronics, impedance matching is the practice of designing the input impedance of an electrical load to maximize the power transfer and/or minimize reflections from the load....
network, the impedances looking in to the network ports bear no relationship to the termination impedances. This means that a network designed by Bartlett's theorem, while having exactly the filter response predicted, also adds a constant attenuation in addition to the filter response. In impedance matching networks, a usual design criteria is to maximise power transfer. The output response is "the same shape" relative to the voltage of the theoretical ideal generator driving the input. It is not the same relative to the actual input voltage which is delivered by the theoretical ideal generator via its load impedance.
The constant gain due to the difference in input and output impedances is given by;
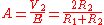
Note that it is possible for this to be greater than unity, that is, a voltage gain is possible, but power is always lost.