.gif)
Topology (electronics)
Encyclopedia
The topology of an electronic circuit is the form taken by the network
of interconnections of the circuit components. Different specific values or ratings of the components are regarded as being the same topology.
Strictly speaking, replacing a component with one of an entirely different type is still the same topology. In some contexts, however, these can loosely be described as different topologies. For instance, interchanging inductors and capacitors in a low-pass filter
results in a high-pass filter. These might be described as high-pass and low-pass topologies even though the network topology is identical. A more correct term for these classes of object (that is, a network where the type of component is specified but not the absolute value) is prototype network
.
, in particular, for networks which contain only two-terminal devices, circuit topology can be viewed as an application of graph theory
. In a network analysis
of such a circuit from a topological point of view, the network nodes
are the vertices
of graph theory and the network branches are the edges of graph theory.
Two networks of this kind have the same topology if, and only if, they both have the same mathematical graph. That is, the same nodes are connected to the same branches in both circuits.
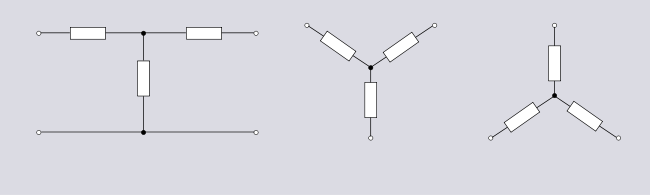This example also demonstrates a common convention of naming topologies after a letter of the alphabet to which they have a resemblance.
.
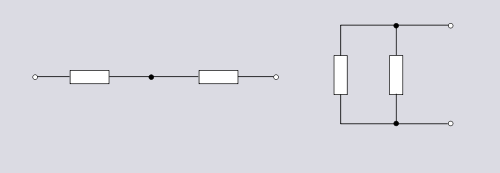Even for these simplest of topologies, there are variations in the way the circuit can be presented.
For a network with three branches there are four possible topologies;
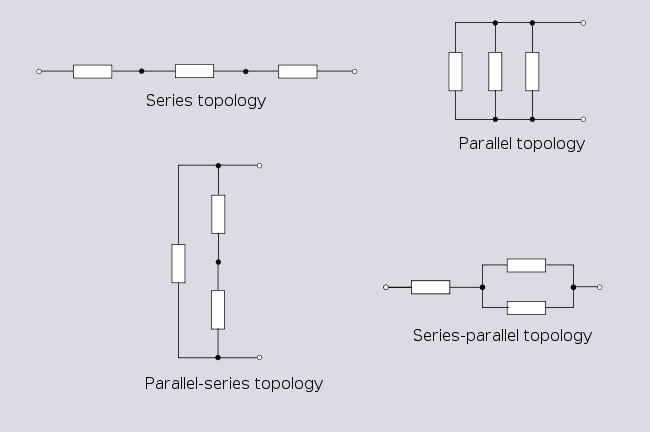Note that the parallel/series topology is another representation of the Delta topology discussed below.
Series and parallel topologies can continue to be constructed with greater and greater numbers of branches ad infinitum. The number of unique topologies that can be obtained from n branches is 2n-1. The total number of unique topologies that can be obtained with no more than n branches is 2n-1.
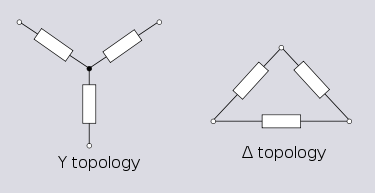Y and Δ are important topologies in linear network analysis due to these being the simplest possible three-terminal networks. A Y-Δ transform is available for linear circuits. This transform is important because there are some networks that cannot be analysed in terms of series and parallel combinations. 
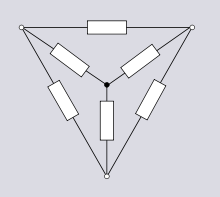For instance, for this network on the left, consisting of a Y network connected in parallel with a Δ network. Say it is desired to calculate the impedance between two nodes of the network. In many networks this can be done by successive applications of the rules for combination of series or parallel impedances. This is not, however, possible in this case where the Y-Δ transform is needed in addition to the series and parallel rules.
The Y topology is also called star topology. However, star topology may also refer to the more general case of many branches connected to the same node.
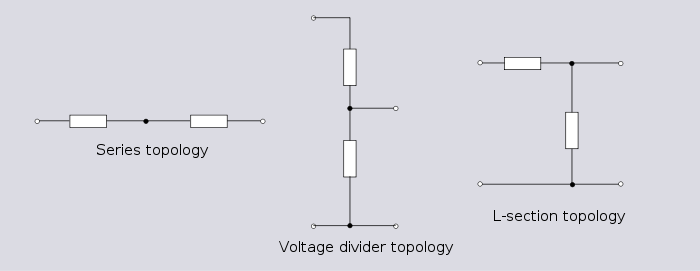
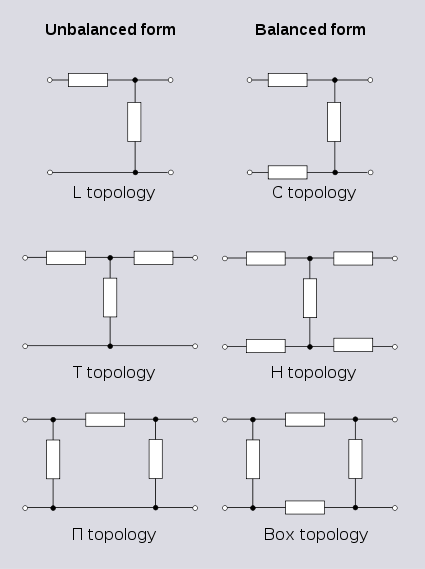The topologies shown opposite are commonly used for filter
and attenuator
designs. The L-section is identical topology to the potential divider topology. The T-section is identical topology to the Y topology. The Π-section is identical topology to the Δ topology.
All these topologies can be viewed as a short section of a ladder topology. Longer sections would normally be described as ladder topology. These kinds of circuits are commonly analysed and characterised in terms of a two-port network
.
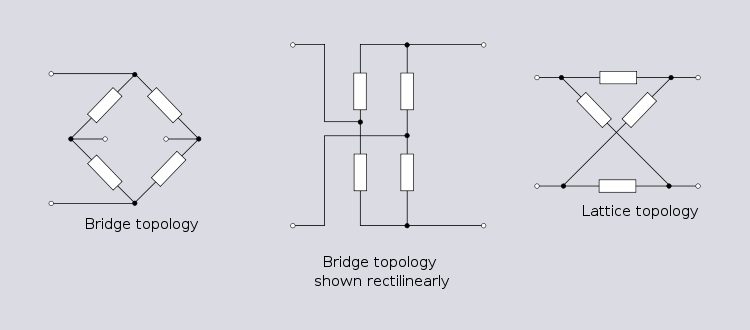Bridge topology is an important topology with many uses in both linear and non-linear applications, including, amongst many others, the bridge rectifier, the Wheatstone bridge
and the lattice phase equaliser
. There are several ways that bridge topology is rendered in circuit diagrams. The first rendering in the diagram above is the traditional depiction of a bridge circuit. The second rendering clearly shows the equivalence between the bridge topology and a topology derived by series and parallel combinations. The third rendering is more commonly known as lattice topology. It is not so obvious that this is topologically equivalent. It can be seen that this is indeed so by visualising the top left node moved to the right of the top right node.
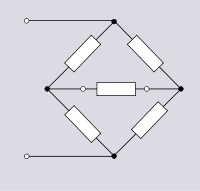It is normal to call a network bridge topology only if it is being used as a two-port network
with the input and output ports each consisting of a pair of diagonally opposite nodes. The box topology in the filter topologies section above can be seen to be identical to bridge topology but in the case of the filter the input and output ports are each a pair of adjacent nodes. Sometimes the loading (or null indication) component on the output port of the bridge will be included in the bridge topology as shown here.
Bridge T topology is derived from bridge topology in a way explained in the Zobel network
article. There are many derivative topologies also discussed in the same article.
There is also a twin-T topology which has practical applications where it is desirable to have the input and output share a common (ground
) terminal. This may be, for instance, because the input and output connections are made with co-axial topology. Connecting together an input and output terminal is not allowable with normal bridge topology and for this reason Twin-T is used where a bridge would otherwise be used for balance or null measurement applications. The topology is also used in the twin-T oscillator as a sine wave generator. The diagram to the left shows twin-T topology redrawn to emphasise the connection with bridge topology.
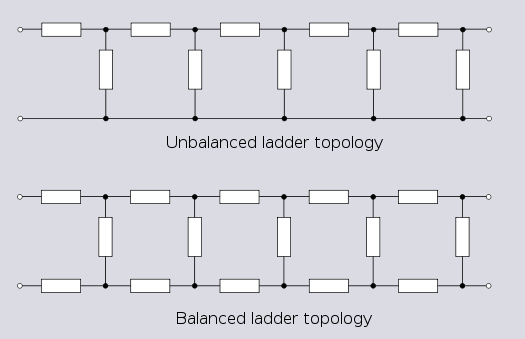Ladder topology can be extended without limit and is much used in filter designs. There are many variations on ladder topology, some of which are discussed in the Electronic filter topology
and Composite image filter
articles.
The balanced form of ladder topology can be viewed as being the graph
of the side of a prism
of arbitrary order. The side of an anti-prism forms a topology which, in this sense, is an anti-ladder. Anti-ladder topology finds an application in voltage multiplier
circuits, in particular the
Cockcroft-Walton generator
. There is also a full-wave version of the Cockcroft-Walton generator which uses a double anti-ladder topology.
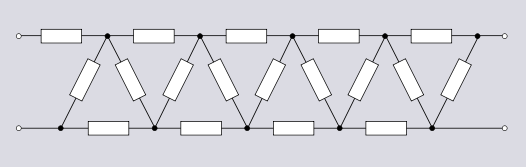
Infinite topologies can also be formed by cascading multiple sections of some other simple topology, such as lattice or bridge-T sections. Such infinite chains of lattice sections occur in the theoretical analysis and artificial simulation of transmission lines, but are rarely used as a practical circuit implementation.
With more complex circuits the description may proceed by specification of a transfer function
between the ports
of the network rather than the topology of the components.
Network analysis (electrical circuits)
A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
of interconnections of the circuit components. Different specific values or ratings of the components are regarded as being the same topology.
Strictly speaking, replacing a component with one of an entirely different type is still the same topology. In some contexts, however, these can loosely be described as different topologies. For instance, interchanging inductors and capacitors in a low-pass filter
Electronic filter
Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
results in a high-pass filter. These might be described as high-pass and low-pass topologies even though the network topology is identical. A more correct term for these classes of object (that is, a network where the type of component is specified but not the absolute value) is prototype network
Prototype filter
Prototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regards to...
.
Mathematical topology
Electronic network topology is related to mathematical topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, in particular, for networks which contain only two-terminal devices, circuit topology can be viewed as an application of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. In a network analysis
Network analysis (electrical circuits)
A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
of such a circuit from a topological point of view, the network nodes
Node (circuits)
In electrical engineering, node refers to any point on a circuit where two or more circuit elements meet. For two nodes to be different, their voltages must be different. Without any further knowledge, it is easy to establish how to find a node by using Ohm's Law: V=IR. When looking at circuit...
are the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
of graph theory and the network branches are the edges of graph theory.
Two networks of this kind have the same topology if, and only if, they both have the same mathematical graph. That is, the same nodes are connected to the same branches in both circuits.
Topology names
Many topology names relate to their appearance when drawn diagramatically. Most circuits can be drawn in a variety of ways and consequently have a variety of names. For instance, the three circuits shown below all look different but have identical topologies.Series and parallel topologies
For a network with two branches, there are only two possible topologies; series and parallelSeries and parallel circuits
Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel and occur very frequently. Components connected in series are connected along a single path, so the same current flows through all of the...
.
Series and parallel topologies can continue to be constructed with greater and greater numbers of branches ad infinitum. The number of unique topologies that can be obtained from n branches is 2n-1. The total number of unique topologies that can be obtained with no more than n branches is 2n-1.
Y and Δ topologies
The Y topology is also called star topology. However, star topology may also refer to the more general case of many branches connected to the same node.
Simple filter topologies
Electronic filter
Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
and attenuator
Attenuator (electronics)
An attenuator is an electronic device that reduces the amplitude or power of a signal without appreciably distorting its waveform.An attenuator is effectively the opposite of an amplifier, though the two work by different methods...
designs. The L-section is identical topology to the potential divider topology. The T-section is identical topology to the Y topology. The Π-section is identical topology to the Δ topology.
All these topologies can be viewed as a short section of a ladder topology. Longer sections would normally be described as ladder topology. These kinds of circuits are commonly analysed and characterised in terms of a two-port network
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
.
Bridge topology
Wheatstone bridge
A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. Its operation is similar to the original potentiometer. It was invented by Samuel Hunter Christie in 1833 and...
and the lattice phase equaliser
Lattice phase equaliser
A lattice phase equaliser or lattice filter is an example of an all-pass filter. That is, the attenuation of the filter is constant at all frequencies but the relative phase between input and output varies with frequency...
. There are several ways that bridge topology is rendered in circuit diagrams. The first rendering in the diagram above is the traditional depiction of a bridge circuit. The second rendering clearly shows the equivalence between the bridge topology and a topology derived by series and parallel combinations. The third rendering is more commonly known as lattice topology. It is not so obvious that this is topologically equivalent. It can be seen that this is indeed so by visualising the top left node moved to the right of the top right node.
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
with the input and output ports each consisting of a pair of diagonally opposite nodes. The box topology in the filter topologies section above can be seen to be identical to bridge topology but in the case of the filter the input and output ports are each a pair of adjacent nodes. Sometimes the loading (or null indication) component on the output port of the bridge will be included in the bridge topology as shown here.
Bridge T and Twin-T topologies
Zobel network
Zobel networks are a type of filter section based on the image impedance design principle. They are named after Otto Zobel of Bell Labs who published a much referenced paper on image filters in 1923. The distinguishing feature of Zobel networks is that the input impedance is fixed in the design...
article. There are many derivative topologies also discussed in the same article.
Ground (electricity)
In electrical engineering, ground or earth may be the reference point in an electrical circuit from which other voltages are measured, or a common return path for electric current, or a direct physical connection to the Earth....
) terminal. This may be, for instance, because the input and output connections are made with co-axial topology. Connecting together an input and output terminal is not allowable with normal bridge topology and for this reason Twin-T is used where a bridge would otherwise be used for balance or null measurement applications. The topology is also used in the twin-T oscillator as a sine wave generator. The diagram to the left shows twin-T topology redrawn to emphasise the connection with bridge topology.
Infinite topologies
Electronic filter topology
Electronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected....
and Composite image filter
Composite image filter
A composite image filter is an electronic filter consisting of multiple image filter sections of two or more different types.The image method of filter design determines the properties of filter sections by calculating the properties they have in an infinite chain of such sections. In this, the...
articles.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
of the side of a prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
of arbitrary order. The side of an anti-prism forms a topology which, in this sense, is an anti-ladder. Anti-ladder topology finds an application in voltage multiplier
Voltage multiplier
thumb|right|280px|Villard cascade voltage multiplier.A voltage multiplier is an electrical circuit that converts AC electrical power from a lower voltage to a higher DC voltage, typically by means of a network of capacitors and diodes....
circuits, in particular the
Cockcroft-Walton generator
Cockcroft-Walton generator
The Cockcroft–Walton generator, or multiplier, is an electric circuit which generates a high DC voltage from a low voltage AC or pulsing DC input...
. There is also a full-wave version of the Cockcroft-Walton generator which uses a double anti-ladder topology.
Infinite topologies can also be formed by cascading multiple sections of some other simple topology, such as lattice or bridge-T sections. Such infinite chains of lattice sections occur in the theoretical analysis and artificial simulation of transmission lines, but are rarely used as a practical circuit implementation.
Components with more than two terminals
Circuits containing components with three or more terminals greatly increase the number of possible topologies. Conversely, the number of different circuits represented by a topology diminishes and in many cases the circuit is easily recognisable from the topology even when specific components are not identified. |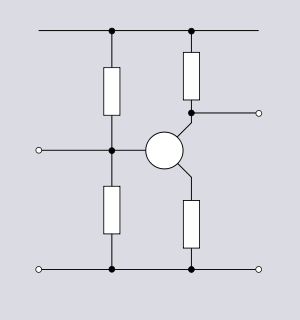
 |
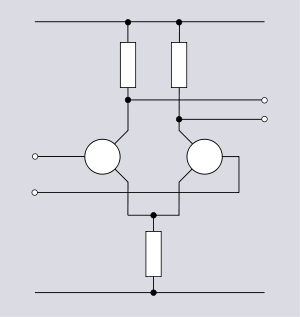With more complex circuits the description may proceed by specification of a transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
between the ports
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
of the network rather than the topology of the components.
See also
- Electronic filter topologyElectronic filter topologyElectronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected....
- Network analysis (electrical circuits)Network analysis (electrical circuits)A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
- Two-port networkTwo-port networkA two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
- Prototype filterPrototype filterPrototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regards to...