Barycentric Julian Date
Encyclopedia
The Barycentric Julian Date (BJD) is the Julian Date (JD) corrected for differences in the Earth
's position with respect to the barycentre of the Solar System
. Due to the finite speed of light
, the time an astronomical event is observed depends on the changing position of the observer in the Solar System. Before multiple observations can be combined, they must be reduced to a common, fixed, reference location. This correction also depends on the direction to the object or event being timed.
In 1991, the BJD replaced the Heliocentric Julian Date (HJD), which reduced times to the centre of the Sun
, which itself orbits the barycentre. The difference between HJD and BJD is up to ±4 s.
. Elsewhere, it is approximately an annual sine curve, and the highest amplitude occurs on the ecliptic. The maximum correction corresponds to the time in which light travels the distance from the barycentre to the Earth, i.e. ±8.3 min (500 s, 0.0058 days).
. JD can be expressed as e.g. UTC
, TT
, TAI
, TDB
, etc. The differences between these time standards are of the order of a minute, so for better than one-minute accuracy, the time standard must be stated. While many quote the BJD in UTC, UTC is discontinuous and drifts with the addition of each leap second
, and should therefore only be used for relative timing over a short time span (~1 year). For high-precision, absolute timing, TDB should be used. However, applications for which ±1.7 ms precision is sufficient may use TT to approximate TDB, which is much easier to calculate.
and general relativity
, the correction of Terrestrial Time
(TT) is
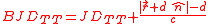
where
is the vector from the barycentre to the observer, 
is the unit vector from the observer to the object or event, 
is the distance from the observer to the observed object or event, and 
is the speed of light.
This expression should be used for objects within the Solar System.
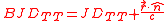
This expression should be used for objects beyond the Solar System. The error is at the level of 100 s for objects in the main asteroid belt, 5 s for Edgeworth-Kuiper Belt objects. At the distance of Proxima Centauri
the accuracy is 1 ms.
numbers are stored in computer
s, the exact expression is in practice not accurate for large distances. The approximation
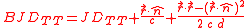
is accurate for large distances. It should be used if the object is beyond the Solar System and if also millisecond accuracy is required.
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's position with respect to the barycentre of the Solar System
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
. Due to the finite speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, the time an astronomical event is observed depends on the changing position of the observer in the Solar System. Before multiple observations can be combined, they must be reduced to a common, fixed, reference location. This correction also depends on the direction to the object or event being timed.
In 1991, the BJD replaced the Heliocentric Julian Date (HJD), which reduced times to the centre of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, which itself orbits the barycentre. The difference between HJD and BJD is up to ±4 s.
Magnitude of the correction
The correction is small for objects at the poles of the eclipticEcliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
. Elsewhere, it is approximately an annual sine curve, and the highest amplitude occurs on the ecliptic. The maximum correction corresponds to the time in which light travels the distance from the barycentre to the Earth, i.e. ±8.3 min (500 s, 0.0058 days).
Time Standard
JD and BJD are defined independent of the time standardTime standard
A time standard is a specification for measuring time: either the rate at which time passes; or points in time; or both. In modern times, several time specifications have been officially recognized as standards, where formerly they were matters of custom and practice. An example of a kind of time...
. JD can be expressed as e.g. UTC
Universal Time
Universal Time is a time scale based on the rotation of the Earth. It is a modern continuation of Greenwich Mean Time , i.e., the mean solar time on the Prime Meridian at Greenwich, and GMT is sometimes used loosely as a synonym for UTC...
, TT
Terrestrial Time
Terrestrial Time is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of the Earth....
, TAI
International Atomic Time
International Atomic Time is a high-precision atomic coordinate time standard based on the notional passage of proper time on Earth's geoid...
, TDB
Barycentric Dynamical Time
Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar system...
, etc. The differences between these time standards are of the order of a minute, so for better than one-minute accuracy, the time standard must be stated. While many quote the BJD in UTC, UTC is discontinuous and drifts with the addition of each leap second
Leap second
A leap second is a positive or negative one-second adjustment to the Coordinated Universal Time time scale that keeps it close to mean solar time. UTC, which is used as the basis for official time-of-day radio broadcasts for civil time, is maintained using extremely precise atomic clocks...
, and should therefore only be used for relative timing over a short time span (~1 year). For high-precision, absolute timing, TDB should be used. However, applications for which ±1.7 ms precision is sufficient may use TT to approximate TDB, which is much easier to calculate.
Exact expression
Neglecting effects of specialSpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the correction of Terrestrial Time
Terrestrial Time
Terrestrial Time is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of the Earth....
(TT) is
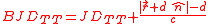
where
is the vector from the barycentre to the observer, is the unit vector from the observer to the object or event, is the distance from the observer to the observed object or event, and is the speed of light.This expression should be used for objects within the Solar System.
Expression for infinite distance
In the limit of infinte distance to the object, the exact expression becomes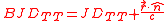This expression should be used for objects beyond the Solar System. The error is at the level of 100 s for objects in the main asteroid belt, 5 s for Edgeworth-Kuiper Belt objects. At the distance of Proxima Centauri
Proxima Centauri
Proxima Centauri is a red dwarf star about 4.2 light-years distant in the constellation of Centaurus. It was discovered in 1915 by Robert Innes, the Director of the Union Observatory in South Africa, and is the nearest known star to the Sun, although it is too faint to be seen with the naked eye...
the accuracy is 1 ms.
Approximation for large distance
Due to the limited precision with which floating pointFloating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
numbers are stored in computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s, the exact expression is in practice not accurate for large distances. The approximation
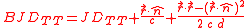
is accurate for large distances. It should be used if the object is beyond the Solar System and if also millisecond accuracy is required.
External links
- http://astroutils.astronomy.ohio-state.edu/time/: Online converter from UTC to BJDTDB, BJDTDB to UTC, or HJD (UTC or TT) to BJDTDB.