Base (group theory)
Encyclopedia
Let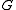 
be a finite permutation group
acting on a set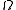
. A sequence
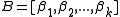
of k distinct elements of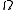
is a base for G if the only element of 
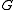which fixes every 
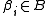pointwise is the identity element of 
.
We define the concept of a strong generating set
relative to a base. Bases and strong generating sets are concepts of importance in computational group theory
. A base and a strong generating set (together often called a BSGS) for a group can be obtained using the Schreier–Sims algorithm.
It is often beneficial to deal with bases and strong generating sets as these may be easier to work with than the entire group. A group may have a small base compared to the set it acts on. In the "worst case", the symmetric group
s and alternating groups have large bases (the symmetric group Sn has base size n − 1), and there are often specialized algorithms that deal with these cases.
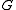be a finite permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
acting on a set
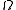. A sequence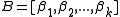of k distinct elements of
is a base for G if the only element of which fixes every 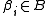pointwise is the identity element of .We define the concept of a strong generating set
Strong generating set
In abstract algebra, especially in the area of group theory, a strong generating set of a permutation group is a generating set that clearly exhibits the permutation structure as described by a stabilizer chain...
relative to a base. Bases and strong generating sets are concepts of importance in computational group theory
Computational group theory
In mathematics, computational group theory is the study ofgroups by means of computers. It is concernedwith designing and analysing algorithms anddata structures to compute information about groups...
. A base and a strong generating set (together often called a BSGS) for a group can be obtained using the Schreier–Sims algorithm.
It is often beneficial to deal with bases and strong generating sets as these may be easier to work with than the entire group. A group may have a small base compared to the set it acts on. In the "worst case", the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s and alternating groups have large bases (the symmetric group Sn has base size n − 1), and there are often specialized algorithms that deal with these cases.