Base flow (random dynamical systems)
Encyclopedia
In mathematics
, the base flow of a random dynamical system
is the dynamical system
defined on the "noise" probability space
that describes how to "fast forward" or "rewind" the noise when one wishes to change the time at which one "starts" the random dynamical system.
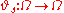on a probability space 
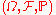. The measure-preserving dynamical system
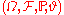is known as the base flow of the random dynamical system. The maps 
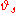are often known as shift maps since they "shift" time. The base flow is often ergodic.
The parameter
may be chosen to run over
Each map
is required
Furthermore, as a family, the maps
satisfy the relations
In other words, the maps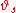
form a commutative monoid
(in the cases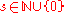
and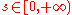 
) or a commutative group
(in the cases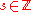
and 
).
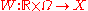, where 
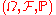is the two-sided classical Wiener space
, the base flow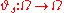
would be given by
.
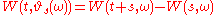This can be read as saying that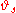
"starts the noise at time 
instead of time 0".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the base flow of a random dynamical system
Random dynamical system
In mathematics, a random dynamical system is a measure-theoretic formulation of a dynamical system with an element of "randomness", such as the dynamics of solutions to a stochastic differential equation...
is the dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
defined on the "noise" probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
that describes how to "fast forward" or "rewind" the noise when one wishes to change the time at which one "starts" the random dynamical system.
Definition
In the definition of a random dynamical system, one is given a family of maps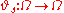 on a probability space 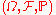. The measure-preserving dynamical systemMeasure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
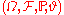is known as the base flow of the random dynamical system. The maps 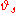are often known as shift maps since they "shift" time. The base flow is often ergodic.The parameter
may be chosen to run over
-
(a two-sided continuous-time dynamical system); -
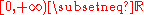(a one-sided continuous-time dynamical system); -
(a two-sided discrete-time dynamical system); -
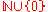(a one-sided discrete-time dynamical system).
Each map
is required
- to be a
-measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
: for all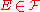
, 
- to preserve the measure
: for all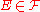 
, 
.
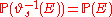Furthermore, as a family, the maps
satisfy the relations
-
, the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on
; -
for all 
and 
for which the three maps in this expression are defined. In particular, 
if 
exists.
In other words, the maps
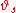form a commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(in the cases
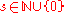and 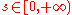) or a commutative groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(in the cases
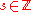and ).Example
In the case of random dynamical system driven by a Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
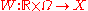, where 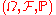is the two-sided classical Wiener spaceClassical Wiener space
In mathematics, classical Wiener space is the collection of all continuous functions on a given domain , taking values in a metric space . Classical Wiener space is useful in the study of stochastic processes whose sample paths are continuous functions...
, the base flow
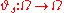would be given by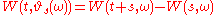.This can be read as saying that
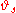"starts the noise at time instead of time 0".