
Basu's theorem
Encyclopedia
In statistics
, Basu's theorem states that any boundedly complete
sufficient statistic is independent
of any ancillary statistic
. This is a 1955 result of Debabrata Basu
.
It is often used in statistics as a tool to prove independence of two statistics, by first demonstrating one is complete sufficient and the other is ancillary, then appealing to the theorem.

The PθA does not depend on θ because A is ancillary. Likewise, Pθ(·|T = t) does not depend on θ because T is sufficient. Therefore we can write:
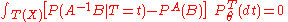
Note the integrand (the function inside the intergal) is a function of t and not θ. Therefore, since T is boundedly complete:
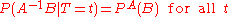
Therefore, A is independent of T.
s with mean
μ and variance
σ2.
Then with respect to the parameter μ, one can show that
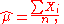
the sample mean, is a complete sufficient statistic – it is all the information one can derive to estimate μ, and no more – and
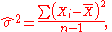
the sample variance, is an ancillary statistic – its distribution does not depend on μ.
Therefore, from Basu's theorem it follows that these statistics are independent.
This independence result can also be proven by Cochran's theorem
.
Further, this property (that the sample mean and sample variance of the normal distribution are independent) characterizes
the normal distribution – no other distribution has this property.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Basu's theorem states that any boundedly complete
Completeness (statistics)
In statistics, completeness is a property of a statistic in relation to a model for a set of observed data. In essence, it is a condition which ensures that the parameters of the probability distribution representing the model can all be estimated on the basis of the statistic: it ensures that the...
sufficient statistic is independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of any ancillary statistic
Ancillary statistic
In statistics, an ancillary statistic is a statistic whose sampling distribution does not depend on which of the probability distributions among those being considered is the distribution of the statistical population from which the data were taken...
. This is a 1955 result of Debabrata Basu
Debabrata Basu
Debabrata Basu was a mathematical statistician who made fundamental contributions to the foundations of statistics. Basu invented simple examples that displayed some difficulties of likelihood-based statistics and frequentist statistics; Basu's paradoxes were especially important in the...
.
It is often used in statistics as a tool to prove independence of two statistics, by first demonstrating one is complete sufficient and the other is ancillary, then appealing to the theorem.
Statement
Let Pθ be a family of distributions on a measurable space (X, Σ). Then if T is a boundedly complete sufficient statistic for θ, and A is ancillary to θ, then T is independent of A.Proof
Let PθT and PθA be the marginal distributions of T and A respectively.
The PθA does not depend on θ because A is ancillary. Likewise, Pθ(·|T = t) does not depend on θ because T is sufficient. Therefore we can write:
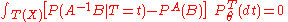
Note the integrand (the function inside the intergal) is a function of t and not θ. Therefore, since T is boundedly complete:
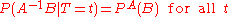
Therefore, A is independent of T.
Independence of sample mean and sample variance of a normal distribution
Let X1, X2, ..., Xn be independent, identically distributed normal random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
μ and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2.
Then with respect to the parameter μ, one can show that
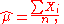
the sample mean, is a complete sufficient statistic – it is all the information one can derive to estimate μ, and no more – and
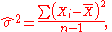
the sample variance, is an ancillary statistic – its distribution does not depend on μ.
Therefore, from Basu's theorem it follows that these statistics are independent.
This independence result can also be proven by Cochran's theorem
Cochran's theorem
In statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used in to justify results relating to the probability distributions of statistics that are used in the analysis of variance.- Statement :...
.
Further, this property (that the sample mean and sample variance of the normal distribution are independent) characterizes
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
the normal distribution – no other distribution has this property.

