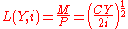Baumol-Tobin model
Encyclopedia
The Baumol-Tobin model is an economic model of the transactions demand
for money as developed independently by William Baumol
(1952) and James Tobin
(1956). The theory relies on the trade off between the liquidity provided by holding money (the ability to carry out transactions) and the interest
foregone by holding one’s assets in the form of non-interest bearing money. The key variables of the demand for money are then the nominal interest rate
, the level of real income which corresponds to the amount of desired transactions and to a fixed cost of transferring one’s wealth between liquid money and interest bearing assets. The model was originally developed in order to provide microfoundations
for aggregate money demand functions commonly used in Keynesian and Monetarist macroeconomic models of the time. Later on, the model was extended to a general equilibrium
setting by Boyan Jovanovic
(1982) and David Romer
(1986).
dollars at the beginning of each period and subsequently spends it at an even rate over the whole period. In order to spend the income she needs to hold some portion of 
in the form of money balances which can be used to carry out the transactions. Alternatively, she can deposit some portion of her income in an interest bearing bank account or in short term bonds. Withdrawing money from the bank, or converting from bonds to money, incurs a fixed transaction cost equal to 
per transfer (which is independent of the amount withdrawn). Let 
denote the number of withdrawals made during the period and assume merely for the sake of convenience that the initial withdrawal of money also incurs this cost. Money held at the bank pays a nominal interest rate,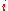 
, which is received at the end of the period. For simplicity, it is also assumed that the individual spends her entire paycheck over the course of the period (there is no saving from period to period).
As a result the total cost of money management is equal to the cost of withdrawals,
, plus the interest foregone due to holdings of money balances,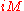 
, where 
is the average amount held as money during the period. Efficient money management requires that the individual minimizes this cost, given her level of desired transactions, the nominal interest rate and the cost of transferring from interest accounts back to money.
The average holdings of money during the period depend on the number of withdrawals made. Suppose that all income is withdrawn at the beginning (N=1) and spent over the entire period. In that case the individual starts with money holdings equal to Y and ends the period with money holdings of zero. Normalizing the length of the period to 1, average money holdings are equal to Y/2. If an individual initially withdraws half her income,
, spends it, then in the middle of the period goes back to the bank and withdraws the rest she has made two withdrawals (N=2) and her average money holdings are equal to 
. In general, the person’s average money holdings will equal 
.
This means that the total cost of money management is equal to:
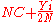
The minimum number of withdrawals can be found by taking the derivative of this expression with respect to
and setting it equal to zero (note that the second derivative is positive, which ensures that this is a minimum, not a maximum).
The condition for minimum is then given by:
Solving this for N we get the optimal number of withdrawals:
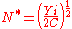
Using the fact that average money holdings are equal to Y/2N we obtain a demand for money function:
The model can be easily modified to incorporate an average price level which turns the money demand function into a demand for liquidity function:
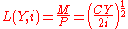
Transactions demand
Transactions demand, in economic theory, specifically Keynesian economics, is one of the determinants of demand for money , the others being speculative demand and precautionary demand. Transactions demand is illustrated as a vertical line on the money demand graph.The demand of money is arisen...
for money as developed independently by William Baumol
William Baumol
William Jack Baumol is an American economist. He is a professor of economics at New York University and is also affiliated with Princeton University. Baumol has written extensively about labor market and other economic factors that affect the economy. He also made valuable contributions to the...
(1952) and James Tobin
James Tobin
James Tobin was an American economist who, in his lifetime, served on the Council of Economic Advisors and the Board of Governors of the Federal Reserve System, and taught at Harvard and Yale Universities. He developed the ideas of Keynesian economics, and advocated government intervention to...
(1956). The theory relies on the trade off between the liquidity provided by holding money (the ability to carry out transactions) and the interest
Interest
Interest is a fee paid by a borrower of assets to the owner as a form of compensation for the use of the assets. It is most commonly the price paid for the use of borrowed money, or money earned by deposited funds....
foregone by holding one’s assets in the form of non-interest bearing money. The key variables of the demand for money are then the nominal interest rate
Nominal interest rate
In finance and economics nominal interest rate or nominal rate of interest refers to the rate of interest before adjustment for inflation ; or, for interest rates "as stated" without adjustment for the full effect of compounding...
, the level of real income which corresponds to the amount of desired transactions and to a fixed cost of transferring one’s wealth between liquid money and interest bearing assets. The model was originally developed in order to provide microfoundations
Microfoundations
In economics, the term microfoundations refers to the microeconomic analysis of the behavior of individual agents such as households or firms that underpins a macroeconomic theory....
for aggregate money demand functions commonly used in Keynesian and Monetarist macroeconomic models of the time. Later on, the model was extended to a general equilibrium
General equilibrium
General equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
setting by Boyan Jovanovic
Boyan Jovanovic
Boyan Jovanovic is a professor of economics at New York University.Jovanovic, of Serbian descent, received his undergraduate education at the London School of Economics and his graduate training at the University of Chicago....
(1982) and David Romer
David Romer
David Romer is the Herman Royer Professor of Political Economy at the University of California, Berkeley, the author of a standard textbook in graduate macroeconomics as well as many influential economic papers, particularly in the area of New Keynesian economics...
(1986).
Formal exposition of the model
Suppose an individual receives her paycheck of dollars at the beginning of each period and subsequently spends it at an even rate over the whole period. In order to spend the income she needs to hold some portion of in the form of money balances which can be used to carry out the transactions. Alternatively, she can deposit some portion of her income in an interest bearing bank account or in short term bonds. Withdrawing money from the bank, or converting from bonds to money, incurs a fixed transaction cost equal to per transfer (which is independent of the amount withdrawn). Let denote the number of withdrawals made during the period and assume merely for the sake of convenience that the initial withdrawal of money also incurs this cost. Money held at the bank pays a nominal interest rate, 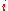, which is received at the end of the period. For simplicity, it is also assumed that the individual spends her entire paycheck over the course of the period (there is no saving from period to period).As a result the total cost of money management is equal to the cost of withdrawals,
, plus the interest foregone due to holdings of money balances, 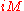, where is the average amount held as money during the period. Efficient money management requires that the individual minimizes this cost, given her level of desired transactions, the nominal interest rate and the cost of transferring from interest accounts back to money.The average holdings of money during the period depend on the number of withdrawals made. Suppose that all income is withdrawn at the beginning (N=1) and spent over the entire period. In that case the individual starts with money holdings equal to Y and ends the period with money holdings of zero. Normalizing the length of the period to 1, average money holdings are equal to Y/2. If an individual initially withdraws half her income,
, spends it, then in the middle of the period goes back to the bank and withdraws the rest she has made two withdrawals (N=2) and her average money holdings are equal to . In general, the person’s average money holdings will equal .This means that the total cost of money management is equal to:
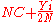
The minimum number of withdrawals can be found by taking the derivative of this expression with respect to
and setting it equal to zero (note that the second derivative is positive, which ensures that this is a minimum, not a maximum).The condition for minimum is then given by:
Solving this for N we get the optimal number of withdrawals:
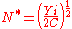
Using the fact that average money holdings are equal to Y/2N we obtain a demand for money function:
The model can be easily modified to incorporate an average price level which turns the money demand function into a demand for liquidity function: