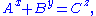Beal's conjecture
Encyclopedia
Beal's conjecture is a conjecture
in number theory
proposed by Andrew Beal
in about 1993; a similar conjecture was suggested independently at about the same time by Andrew Granville
.
While investigating generalizations of Fermat's last theorem
in 1993, Beal formulated the following conjecture:
If
where A, B, C, x, y, and z are positive integers with x, y, z > 2 then A, B, and C must have a common prime factor
.
Beal has offered a prize of US$100,000 for a proof of his conjecture or a counterexample.
for any ,
,  ,
,  . But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor
. But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor 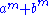 in common.
in common.
The example 73 + 132 = 29 shows that the conjecture is false if one of the exponents is allowed to be 2.
, this conjecture has been verified for all values of all six variables
up to 1000. So in any counterexample
, at least one of the variables must be greater than 1000.
A variation of the conjecture where x, y, z (instead of A, B, C) must have a common prime factor is not true. See, for example .
.
Beal's conjecture is a generalization of Fermat's last theorem, which corresponds to the case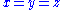 . If
. If 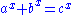 with
with  , then either the bases are coprime
, then either the bases are coprime
or share a common factor. If they share a common factor, it can be divided out of each to yield an equation with smaller, coprime bases.
The conjecture is not valid over the larger domain of Gaussian integers. After a prize of $50 was offered for a counterexample, Fred W. Helenius provided (−2 + i)3 + (−2 − i)3 = (1 + i)4.
In addition with Beal Conjecture, here is the remodeled form of Sinha Conjecture:
Excogitation & Innovation Laboratory has announced an award of US $150,000.00 in June 9, 2009 (the award money is made triple in January 11, 2010), for the proof or disproof of the Sinha Conjecture.
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
proposed by Andrew Beal
Andrew Beal
D. Andrew "Andy" Beal is a Dallas, Texas-based billionaire businessman who was born and raised in Lansing, Michigan. He made his fortune in banking and real estate and is the founder and chairman of Beal Bank and Beal Aerospace Technologies. Beal is also known for his high-stakes poker games and...
in about 1993; a similar conjecture was suggested independently at about the same time by Andrew Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
.
While investigating generalizations of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
in 1993, Beal formulated the following conjecture:
If
where A, B, C, x, y, and z are positive integers with x, y, z > 2 then A, B, and C must have a common prime factor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
.
Beal has offered a prize of US$100,000 for a proof of his conjecture or a counterexample.
Examples
To illustrate, the solution 33 + 63 = 35 has bases with a common factor of 3, and the solution 76 + 77 = 983 has bases with a common factor of 7. Indeed the equation has infinitely many solutions, including for examplefor any
 ,
,  ,
,  . But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor
. But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor 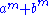 in common.
in common.The example 73 + 132 = 29 shows that the conjecture is false if one of the exponents is allowed to be 2.
Properties
By computerized searching, greatly accelerated by aid of modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, this conjecture has been verified for all values of all six variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
up to 1000. So in any counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
, at least one of the variables must be greater than 1000.
A variation of the conjecture where x, y, z (instead of A, B, C) must have a common prime factor is not true. See, for example
 .
.Beal's conjecture is a generalization of Fermat's last theorem, which corresponds to the case
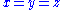 . If
. If 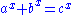 with
with  , then either the bases are coprime
, then either the bases are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
or share a common factor. If they share a common factor, it can be divided out of each to yield an equation with smaller, coprime bases.
The conjecture is not valid over the larger domain of Gaussian integers. After a prize of $50 was offered for a counterexample, Fred W. Helenius provided (−2 + i)3 + (−2 − i)3 = (1 + i)4.
Sinha Conjecture Prize
But, Andrew Beal has found only two possibilities, whereas there has been remained other two possibilities of FLT, which has found by Neil Sinha, another non-mathematician.In addition with Beal Conjecture, here is the remodeled form of Sinha Conjecture:
Let X, Y, Z, a, b, and c be positive integers, with a, b, c > 2. Whether X and Y have a common factor or not, the equation Xa + Yb = Zc has a solution if:
- at least any one of X and Y is coprime
CoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to Z, when X and Y coprime;
and the equation Xa + Yb = Zc has no solution if:
- at least any one of X and Y is coprime with Z, when X and Y have a common factor.
Excogitation & Innovation Laboratory has announced an award of US $150,000.00 in June 9, 2009 (the award money is made triple in January 11, 2010), for the proof or disproof of the Sinha Conjecture.
External links
- http://www.bealconjecture.com/
- http://www.math.unt.edu/~mauldin/beal.html
- http://mathoverflow.net/questions/28764/status-of-beal-tijdeman-zagier-conjecture
- Sinha Conjecture http://www.eilab.org/sinha.htm http://www.eilab.org/sinha.htm